Growth And Consequences In New York City's School Rating System
In a New York Times article a couple of weeks ago, reporter Michael Winerip discusses New York City’s school report card grades, with a focus on an issue that I have raised many times – the role of absolute performance measures (i.e., how highly students scores) in these systems, versus that of growth measures (i.e., whether students are making progress).
Winerip uses the example of two schools – P.S. 30 and P.S. 179 – one of which (P.S. 30) received an A on this year’s report card, while the other (P.S. 179) received an F. These two schools have somewhat similar student populations, at least so far as can be determined using standard education variables, and their students are very roughly comparable in terms of absolute performance (e.g., proficiency rates). The basic reason why one received an A and the other an F is that P.S. 179 received a very low growth score, and growth is heavily weighted in the NYC grade system (representing 60 out of 100 points for elementary and middle schools).
I have argued previously that unadjusted absolute performance measures such as proficiency rates are inappropriate for test-based assessments of schools' effectiveness, given that they tell you almost nothing about the quality of instruction schools provide, and that growth measures are the better option, albeit one that also has its own issues (e.g., they are more unstable), and must be used responsibly. In this sense, the weighting of the NYC grading system is much more defensible than most of its counterparts across the nation, at least in my view.
But the system is also an example of how details matter – each school’s growth portion is calculated using an unconventional, somewhat questionable approach, one that is, as yet, difficult to treat with a whole lot of confidence.
The process for generating schools’ growth scores may seem complex on the surface, but the calculations are for the most part pretty simple. If you’ll bear with me, they’re worth reviewing, as they’re important for getting a sense as to what the final numbers actually mean.
- First, every student’s original scale score is converted to the state’s standard “proficiency rating” (a continuous measure that ranges between 1.0-4.5), in order to make them comparable between grades. This is a potential question, right off the bat, as it is essentially imposing a somewhat untested structure on the scores, one that is not necessarily well-suited for these comparisons.*
- Second, in the most important step, each student’s proficiency rating is compared with those of students who were at similar levels last year, producing a percentile that represents the percent of students who scored lower in 2011 but started out at the same level in 2010. Some version of this technique is used in several states, though it has come under criticism when used for high-stakes accountability, given that it is (arguably) designed to describe the performance of students, rather than isolate the effect of schools on their students’ performance. If you share my opinion that growth-based measures are preferable, then this technique is still better than absolute performance measures, but I for one would like to see how the results compare with those of different models, particularly value-added models proper.**
- Third, that percentile score – for each student - is “adjusted” for student characteristics, namely poverty and special education. Put simply, students’ percentiles are increased by a set amount depending on their special education classification (e.g., self-contained), as well as on their schools’ Title I enrollment. The adjustment amounts, according to the city, are supposed to represent the average difference in growth for each of these groups of students, but the amounts are predetermined and don’t vary between years, school types (elementary/middle) or subject (whereas the actual differences presumably do). It's therefore difficult to say what they actually represent. Making these kinds of adjustments is important and it should be done (often by the model itself, rather than after the fact), but this strikes me as a slapdash way to do it. It’s difficult to tell, and the city provides no detailed documentation (that I could find).
- Fourth, after these adjustments, the students are sorted, and the median represents the school’s growth percentile. Each school’s median is compared with its “peer group," which are schools that are similar in terms of demographics, as well as with all schools in the city (the former is weighted more heavily, though the two scores are highly correlated). A simple formula converts the scores into point totals.***
- Finally, the whole process is also repeated for the school’s lowest-scoring one-third of students within each grade/subject (which is also compared with peer schools and all city schools). The idea of overweighting the performance of the lowest-scoring students may be a good one in theory, but most of these are based on the tiniest samples – often around 20-50 students (P.S. 179, the school that received an F, had half its 60 growth points based on a sample of 35 students in ELA, 34 in math). In many cases, these samples are too small to be included (especially since, as mentioned below, their error margins are not considered).
There are always questions about the validity these types of measures, no matter how they're done, but the city's approach is particularly vulnerable to this charge. Given all the issues embedded in the process above, it’s tough to know what the numbers mean - i.e., whether they can be regarded as approximate causal effects. Serious caution is well-advised.
(It’s also worth noting that schools’ final numerical scores are categorized into A-F grades in a manner that ensures a certain distribution – 25 percent of schools necessarily receive A’s, 35 percent B’s, 30 percent C’s, 7 percent D’s and 5 percent F’s.)
One simple, albeit rough way to see how well the growth model is accounting for factors outside of schools' control is to check whether the scores are associated with (i.e., possibly biased by) any student characteristics. They are.
The size, direction and statistical significance of these differences vary by characteristic and school type. For instance, elementary schools with larger proportions of special education and black/Hispanic students tend to get lower growth scores. On the other hand, there is minimal bias in growth scores by school-level free/reduced-price lunch eligibility.
(My quick models match up with the solid, more thorough work done by the city's Independent Budget Office, which I found after drafting this post.)
These associations (some are statistically discernible but not large) may stem from the simplicity of the city’s model, which attempts to control for student characteristics by limiting each student’s comparison group to those with the same score last year (i.e., controlling for prior achievement), as well as by comparing schools with their peer groups (which have similar student populations). These methods do absorb some of the bias in the growth estimates (and the relatively heavy weighting of growth means that the final ratings are less biased than in most other systems, which rely more on absolute performance), but not all of it.
These statistical associations - between schools' growth scores and their students' characteristics - do not necessarily represent evidence that the ratings are "inaccurate," but they are certainly cause for serious concern and further investigation.
Another issue with the NYC growth measures, albeit one that is common in these grading systems, is that there is only a rudimentary attempt to account for measurement error - the scores are mostly taken at face value. As a result, for example, it’s quite possible that a large portion of schools’ growth scores are not statistically different from one another - i.e., that some part of the variation in schools' scores is due to nothing more than random chance.
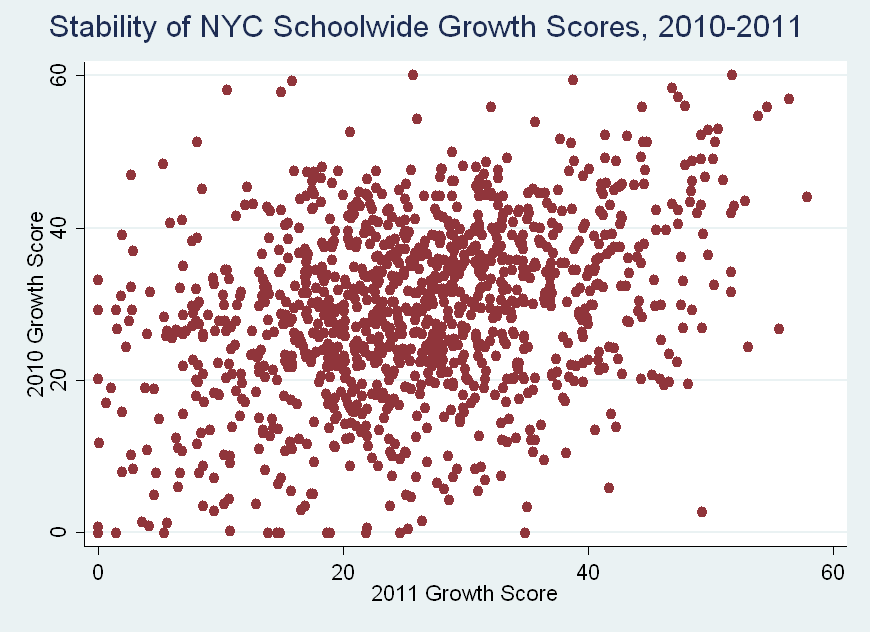
One back-of-the-envelope way to assess the error is to see how stable the estimates are between years – if there’s greater imprecision, a school’s scores will fluctuate more between years. Take a look at the scatterplot below. Each dot is a school (not separated by school type). On the horizontal axis is each school’s 2009-10 growth score, while the vertical is the same measure the next year – in 2010-11 (note that the calculations are slightly different between years, but similar enough for this comparison).
The year-to-year correlation is 0.339, which is generally considered on the low end of moderate. At least some, and probably most of this instability is not "real" - i.e., it is due to imprecision in the estimates, rather than actual changes in school performance.
(Last year, P.S. 179, the school that received an F this year because its growth score was essentially zero, got 11 out of 60 growth points, making for a final grade of C.)
To reiterate, this issue of error and instability in the school growth measures is inevitable and does not, by itself, preclude the usefulness of the measures, but it is exacerbated by the fact that NYC only uses one-year estimates, and the samples of students used for these calculations are, as usual, really quite small (this is especially true for the estimates of growth among the "lowest-performing one third" of students, which probably drive much of this overall instability).
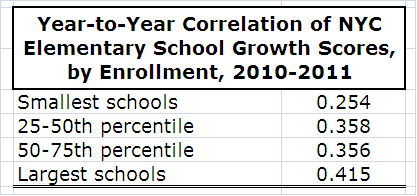
For example, the table below presents the stability in overall growth scores between 2009-10 and 2010-11 by school size (a decent approximation of test-taker sample size), sorted in quartiles. Since schools' enrollment varies by type (e.g., middle schools tend to be smaller), I limit the illustration to elementary schools only.
As expected, scores were considerably more stable in larger schools (though still moderately so). In the city’s smallest elementary schools, the year-to-year correlation (0.254) is relatively low (both P.S. 30 and P.S. 179 are in the second smallest quartile). Stability is similar among schools in the two middle quartiles, because enrollment doesn't vary that much in the middle of the distribution.
Larger samples would improve reliability, and this could be accomplished by averaging together 2-3 years for each school on a rolling basis.
Overall, in my view, NYC’s system takes the right approach insofar as it weights growth more heavily than absolute performance, but the details of the growth measure are therefore very important, and the city’s methods have a “thrown together” feel to them. There is a larger-than-usual degree to which they may be describing students' progress on tests, rather than isolating schools' actual effects on that progress. One can only hope that these state and city grading systems are a work in progress.
In the meantime, I would regard the school grades – including those for P.S. 30 and P.S. 179 – with skepticism. Unfortunately, given the potential stakes attached to these grades, the schools don’t always have that luxury.
- Matt Di Carlo
*****
* The unconventional nature of the city’s approach is reflected in the fact that NYS as a whole, per its NCLB waiver application, will not be using the proficiency-based transformation, but rather a more common metric (z-scores).
** It’s not clear whether this process is done via modeling (e.g., quantile regression) or just manually – separating students by starting score, and sorting them by their ending scores. One has to assume the former, but if the latter is the case, then this is additional cause for concern.
*** The peer group score (as well as the score compared with all city schools) represents the relative standing (as a percentage) of the school within a range, with that range defined as scores within two standard deviations of the mean. The idea here is sound – one should compare schools with similar “peer” schools, but one alternative would be to "bake" these comparisons into the model itself.