Reign Of Error: The Publication Of Teacher Data Reports In New York City
Late last week and over the weekend, New York City newspapers, including the New York Times and Wall Street Journal, published the value-added scores (teacher data reports) for thousands of the city’s teachers. Prior to this release, I and others argued that the newspapers should present margins of error along with the estimates. To their credit, both papers did so.
In the Times’ version, for example, each individual teacher’s value-added score (converted to a percentile rank) is presented graphically, for math and reading, in both 2010 and over a teacher’s “career” (averaged across previous years), along with the margins of error. In addition, both papers provided descriptions and warnings about the imprecision in the results. So, while the decision to publish was still, in my personal view, a terrible mistake, the papers at least make a good faith attempt to highlight the imprecision.
That said, they also published data from the city that use teachers’ value-added scores to label them as one of five categories: low, below average, average, above average or high. The Times did this only at the school level (i.e., the percent of each school’s teachers that are “above average” or “high”), while the Journal actually labeled each individual teacher. Presumably, most people who view the databases, particularly the Journal's, will rely heavily on these categorical ratings, as they are easier to understand than percentile ranks surrounded by error margins. The inherent problems with these ratings are what I’d like to discuss, as they illustrate important concepts about estimation error and what can be done about it.
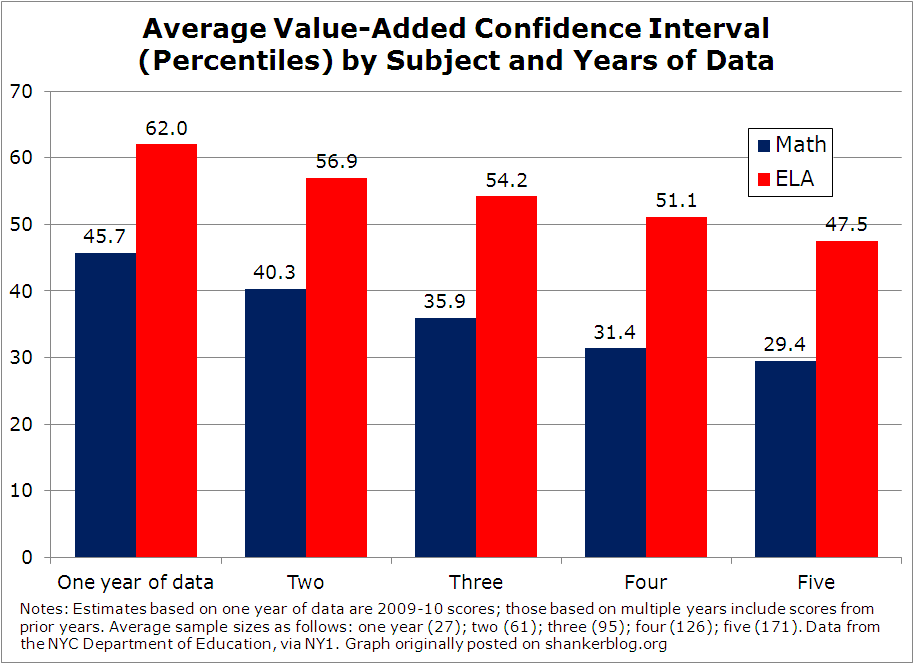
First, let’s quickly summarize the imprecision associated with the NYC value-added scores, using the raw datasets from the city. It has been heavily reported that the average confidence interval for these estimates – the range within which we can be confident the “true estimate” falls - is 35 percentile points in math and 53 in English Language Arts (ELA). But this oversimplifies the situation somewhat, as the overall average masks quite a bit of variation by data availability. Take a look at the graph below, which shows how the average confidence interval varies by the number of years of data available, which is really just a proxy for sample size (see the figure's notes).
When you’re looking at the single-year teacher estimates (in this case, for 2009-10), the average spread is a pretty striking 46 percentile points in math and 62 in ELA. Furthermore, even with five years of data, the intervals are still quite large – about 30 points in math and 48 in ELA. (There is, however, quite a bit of improvement with additional years. The ranges are reduced by around 25 percent in both subjects when you use five years data compared with one.)
Now, opponents of value-added have expressed a great deal of outrage about these high levels of imprecision, and they are indeed extremely wide – which is one major reason why these estimates have absolutely no business being published in an online database. But, as I’ve discussed before, one major, frequently-ignored point about the error – whether in a newspaper or an evaluation system – is that the problem lies less with how much there is than how you go about addressing it.
It’s true that, even with multiple years of data, the estimates are still very imprecise. But, no matter how much data you have, if you pay attention to the error margins, you can, at least to some degree, use this information to ensure that you’re drawing defensible conclusions based on the available information. If you don’t, you can't.
This can be illustrated by taking a look at the categories that the city (and the Journal) uses to label teachers (or, in the case of the Times, schools).
Here’s how teachers are rated: low (0-4th percentile); below average (5-24); average (25-74); above average (75-94); and high (95-99).
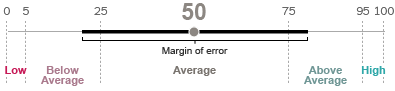
To understand the rocky relationship between value-added margins of error and these categories, first take a look at the Times’ “sample graph” below.
This is supposed to be a sample of one teacher’s results. This particular hypothetical teacher’s value-added score was at the 50th percentile, with a margin of error of plus or minus roughly 30 percentile points. What this tells you is that we can have a high level of confidence that this teacher’s “true estimate” is somewhere between the 20th and 80th percentile (that’s the confidence interval for this teacher), although it is more likely to be closer to 50 than 20 or 80.
One shorthand way to see whether teachers scores are, accounting for error, average, above average or below average is to see whether their confidence intervals overlap with the average (50th percentile, which is actually the median, but that's a semantic point in these data).
Let’s say we have a teacher with a value-added score at the 60th percentile, plus or minus 20 points, making for a confidence interval of 40-80. This crosses the average/median “border," since the 50th percentile is within the confidence interval. So, while this teacher, based on his or her raw percentile rank, may appear to be above the average, he or she cannot really be statistically distinguished from average (because the estimate is too imprecise for us to reject the possibility that random error is the only reason for the difference).
Now, let’s say we have another teacher, scoring at the 60th percentile, but with a much smaller error margin of plus or minus 5 points. In this case, the teacher is statistically above average, since the confidence interval (55-65) doesn’t cross the average/median border.
The big point here is that each teacher’s actual score (e.g., 60th percentile) must be interpreted differently, using the error margins, which vary widely between teachers. The fact that our first teacher had a wide margin of error (20 percentile points) did not preclude accuracy, since we used that information to interpret the estimate, and the only conclusion we could reach was the less-than-exciting but accurate characterization of the teacher as not distinguishable from average.
There’s always error, but if you pay attention to each teacher’s spread individually, you can try to interpret their scores more rigorously (though it's of course no guarantee).
Somewhat in contradiction with that principle, the NYC education department’s dataset sets its own uniform definitions of average (the five categories mentioned above), which are reported by the Times (at the school-level) and Journal (for each teacher). The problem is that the cutpoints are the same for all teachers – i.e., they largely ignore variability in margins of error.*
As a consequence, a lot of these ratings present misleading information.
Let’s see how this works out with the real data. For the sake of this illustration, I will combine the “high” and “above average” categories, as well as the “low” and “below average” categories. This means our examination of the NYC scheme’s "accuracy" – at least by the alternative standard accounting for error margins – is more lenient, since we’re ignoring any discrepancies among teachers assigned to categories at the very top and very bottom of the distribution.
When you rate teachers using the NYC scheme, about half of the city’s teachers receive “average," about a quarter received “below average” or “low," and the other quarter got “above average” or “high." This of course makes perfect sense – by definition, about half of teachers would come in between the 25th and 50th percentiles, so about half would be coded as “average."
Now, let’s look at the distribution of teacher ratings when you actually account for the confidence intervals – i.e., when you define average, above average, and below average in terms of whether estimates are statistically different from the average – i.e., whether the confidence intervals overlap with the average/median.
Since sample size is a big factor here, I once again present the distribution two different ways for each subject. One of them (“multi-year”) is based on teachers’ “career” estimates, limited to those that include between 2-5 years of data. The other is on their 2010 (single-year) estimates alone. In general, the former will be more accurate (i.e., will yield a more narrow confidence interval) than the latter.
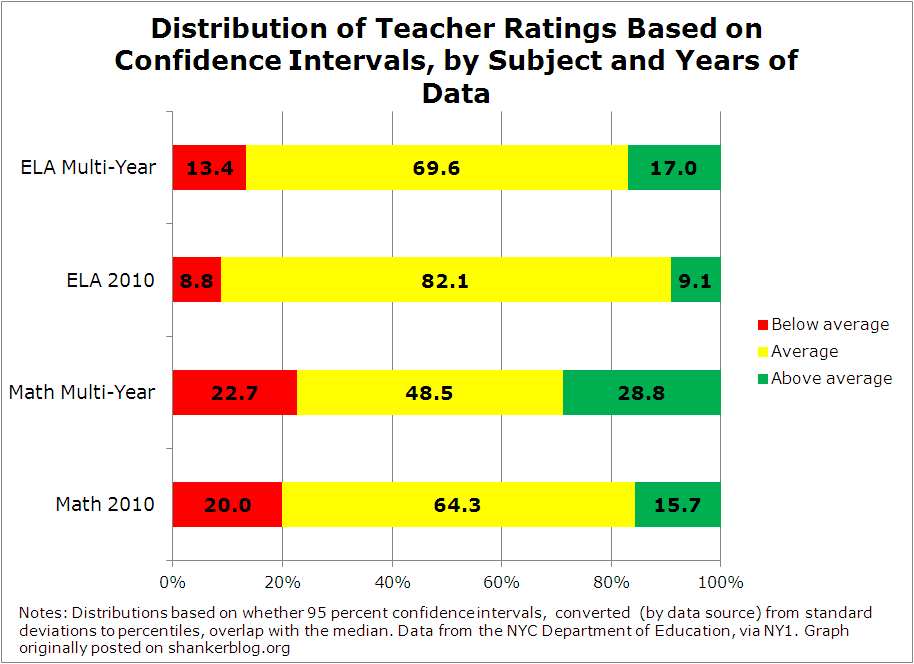
These figures tell us the percentages of teachers’ scores that we can be confident are above average (green) or below average (red), as well as those that we cannot say are different from average (yellow). In many respects, only the estimates that are statistically above or below average are “actionable” – i.e., they’re the only ones that actually provide any information that might be used in policy (or by parents). All other teachers’ scores are best interpreted as no different from average – not in the negative sense of that term, but rather in the sense that the available data do not permit us to make a (test-based) determination that they are anything other than normally competent professionals.
There are three findings to highlight in the graph. First, because the number of years of data makes a big difference in precision (as shown in the first graph), it also influences how many teachers can actually be identified as above or below average (by the standard I’m using). In math, when you use the multi-year estimates (i.e., those based on 2-5 years of data), the distribution is quite similar to the modified NYC categories, with roughly half of teachers classified as indistinguishable from the average (this actually surprised me a bit, as I thought it would be higher).
When you use only one year of data, however, almost two-thirds cannot be distinguished from average. You get a similar decrease in ELA (from 82.1 percent to 69.6 percent).
In other words, when you have more years of data, more teachers’ estimates are precise enough, one way or the other, to draw conclusions. This illustrates the importance of sample size (years of data) in determining how much useful information these estimates can provide (and the potential risk of ignoring it).
The second thing that stands out from the graph, which you may have already noticed, is the difference between math and ELA. Even when you use multiple years of data, only about three in ten ELA teachers’ estimates are discernibly above or below average, whereas the proportion in math is much higher. This tells you that value-added scores in ELA are subject to higher levels of imprecision than those in math, and that even when there are several years of data, most teachers’ ELA estimates are statistically indistinguishable from the average.
This is important, not only for designing evaluation systems (discussed here), but also for interpreting the estimates in the newspapers’ databases. If you don't pay attention to error, the same percentile rank can mean something quite different in math versus ELA in terms of precision, even across groups of teachers (e.g., schools). And, beyond the databases, the manner in which the estimates are incorporated along with other measures into systems such as evaluations - for example, whether you use percentile ranks or actual scores (usually, in standard deviations) - is very important, and can influence the final results.
The third and final takeaway here – and the one that’s most relevant to the public databases – is that the breakdowns in the graph are in most cases quite different from the breakdowns using the NYC system (in which, again, about half of teachers are “average," and about a quarter are coded as “above-" and “below average”).
In other words, the NYC categories might in many individual cases be considered misleading. Many teachers who are labeled as “above average” or “below average” by the city are not necessarily statistically different from the average, once the error margins are accounted for. Conversely, in some cases, teachers who are rated average in the NYC system are actually statistically above or below average – i.e., their percentile ranks are above or below 50, and their confidence intervals don’t overlap with the average/median.
In the graph below, I present the percent of teachers whose NYC ratings would be different under the scheme that I use – that is, they are coded in the teacher data reports as “above average” or “below average” when they are (by my ratings, based on confidence intervals) no different from average, or vice-versa.
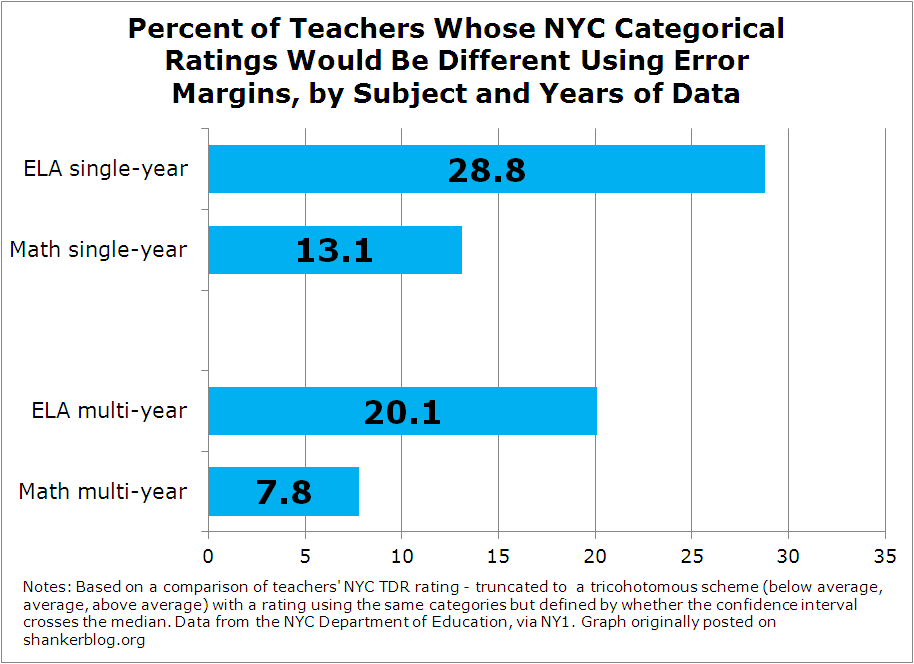
The discrepancies actually aren’t terrible in math – about eight percent with multiple years of data, and about 13 percent when you use a single year (2010). But they’re still noteworthy. About one in ten teachers is given a label – good or bad – that is based on what might be regarded as a misinterpretation of statistical estimates.
In ELA, on the other hand, the differences are rather high – one in five teachers gets a different rating using multiple years of data, compared with almost 30 percent based on the single-year estimates.
And it’s important to reiterate that I’m not even counting the estimates categorized as “low” (0-5th percentile) or “high” (95-99th percentile). If I included those, the rates in the graph would be higher.
(Side note: At least in the older versions of the NYC teacher data reports [sample here], there is actually an asterisk placed next to any teacher’s categorical rating that is accompanied by a particularly wide margin of error, along with a warning to “interpret with caution." I'm not sure - but hope - this practice continued in the more recent versions, but, either way, the asterisks do not appear in the newspaper databases, which I assume is because they are not included in the datasets that the papers received.)
I feel it was irresponsible to publish the NYC categories. I can give a pass to the Times, since they didn’t categorize each teacher individually (only across schools). The Journal, on the other hand, did choose to label each teacher, even using estimates that are based on only year of data – most of which are, especially for ELA, just too imprecise to be meaningful, regardless of whether or not the error margins were presented too. These categorical ratings, in my opinion, made a bad situation worse.
That said, you might argue that I’m being unfair here. Both papers did, to their credit, present and explain the error margins. Moreover, in choosing an alternative categorization scheme, the newspapers would have had to impose their own judgment on data that they likely felt a responsibility to provide to the public as they were received. Put differently, if the city felt the categorical ratings were important and valid, then it might be seen as poor journalistic practice, perhaps even unethical, to alter them.
That’s all fair enough – this is just my opinion, and the importance of this issue pales in comparison with the (in my view, wrong) decision to publish in the first place. But I would point out that the Times did make the choice to withhold the categories for individual teachers, so at least one newspaper felt omitting them was the right thing to do.
(On a related note, the Los Angeles Times value-added database, released in 2010, also applied labels to individual teachers, but they actually required that teachers have at least 60 students before publishing their names. Had the NYC papers applied the LA Times’ standard, they would have withheld almost 30 percent of teachers’ multi-year scores, and virtually all of their single-year scores.)
In any case, if there’s a bright spot to this whole affair, it is the fact that value-added error margins are finally getting the attention they are due.
And, no matter what you think of the published categorical ratings (or the decision to publish the database), all the issues discussed above – the need to account for error margins, the importance of sample size, the difference in results between subjects, etc. – carry very important implications for the use of value-added and other growth model estimates in evaluations, compensation, and other policy contexts. Although many systems are still on the drawing board, most of the new evaluations now being rolled out make the same "mistakes" as are reflected in the newspaper databases.**
So, I’m also hoping that more people will start asking the big question: If the error margins are important to consider when publishing these estimates in the newspaper, why are they still being ignored in most actual teacher evaluations?
In a future post, I’ll take a look at other aspects of the NYC data.
- Matt Di Carlo
*****
* It’s not quite accurate to say that these categories completely ignore the error margins, since they code teachers as average if they’re within 25 percentile points of the median (25-75). In other words, they don’t just call a teacher “below average” if he or she has a score below 50. They do allow for some spread, but it’s just the same for all teachers (the extremely ill-advised alternative is to code teachers as above average if they’re above 50, below if they’re below). One might also argue that there’s a qualitative difference between, on the hand, the city categorizing its teachers in reports that only administrators and teachers will see, and, on the other hand, publishing these ratings in the newspaper.
** In fairness, there are some (but very few) exceptions, such as Hillsborough County, Florida, which requires that teachers have at least 60 students for their estimates to count in formal evaluations. In addition, some of the models being used, such as D.C.’s, use a statistical technique called “shrinking," by which estimates are adjusted according to sample size. If any readers know of other exceptions, please leave a comment.

Matthew-
Thanks very much for this very informative post. You have done a great service pointing out the importance of error margins in the interpretation of these scores. However, as I have followed your commentary (and Bruce Baker's) on the limitations of value-added assessment, it seems that there are many other methodological concerns that should also be raised as part of this discussion. Let me begin by noting that I have no knowledge of the specific VAMs used by NYC to calculate these results.
If possible, I would like you to comment on the other methodological caveats that should be considered when one attempts to evaluate the ultimate meaning of these scores, i.e., not only their precision, but also their underlying validity.
Here’s my incomplete list.
1. Does the VAM used to calculate the results plausibly meet its required assumptions? Did the contractor test this? (See Harris, Sass, and Semykina, “Value-Added Models and the Measurement of Teacher Productivity” Calder Working Paper No. 54.)
2. Was the VAM properly specified? (e.g., Did the VAM control for summer learning, tutoring, test for various interactions, e.g., between class size and behavioral disabilities?)
3. What specification tests were performed? How did they affect the categorization of teachers as effective or ineffective?
4. How was missing data handled?
5. How did the contractors handle team teaching or other forms of joint teaching for the purposes of attributing the test score results?
6. Did they use appropriate statistical methods to analyze the test scores? (For example, did the VAM provider use regression techniques if the math and reading tests were not plausibly scored at an interval level?)
7. When referring back to the original tests, particularly ELA, does the range of teacher effects detected cover an educationally meaningful range of test performance?
8. To what degree would the test results differ if different outcome tests were used?
9. Did the VAM provider test for sorting bias?
My overall point is that measurement precision is very important, but let’s also consider the other reasons why these VAM results should be read with great caution.
Thanks again.
Harris
Matt,
Overall, I think you've done us a great service by digging more deeply into the labels and the meanings of different estimates and calculations. I also think everything Harris Zwerling noted above (in his "incomplete" list) presents insurmountable problems for the use of VAM to evaluate teachers given the available data.
Also, if we change some significant variables in the context and conditions surrounding the teacher's work from year to year, then haven't the relevant data been produced in different ways, rendering them much more difficult, if not impossible, to compare, or to blend into a single calculation? And do you know any teachers for whom conditions are held constant from one year to the next? If our goal is to compare teachers, can we assume that changes in conditions each year affect each teacher in the same way?
And finally, a stylistic request: a few times above you used the data and labels to say that "the teacher is" average, above, below, etc. I don't think you mean to suggest that these tests actually tell us what the teacher's overall quality or skill might be. "An average teacher" in this situation is more precisely "a teacher whose students produced average test score gains." I think it's important not to let our language and diction drift, lest our thoughts become similarly muddled on this topic.
I think one more thing to consider here might be the psychology of interpreting statistics.
Those like yourself who have advanced statistics training have extensive experience in ignoring certain tendencies, or looking at numbers in different ways that most people do.
For example, it might be true and seemingly honest that to say that a teacher scored on the 27th percentile, which, with a 53% margin of error is not statistically different from average. But when people read 27 + or minus 53, they are given the impression of precise measurements (look, they are even precise in their margin of error!). I know that the margin of error as a statistical concept is calculated in a certain way, but that is not how most people understand it. To me, this is similar to reporting way too many decimal places, giving a reader an overly precise estimate. I could say that my car gets 27.567 miles per gallon, with a margin of error of 3.023, or I could say that it gets around 25 or 30 miles per gallon. These might be equivalent to someone with statistics training, but they are not to most people.
Anyways, good reading as always.
This was a very good post on the reliability of the data published, but I don't think it goes far enough to cast a shadow over the numbers themselves.
First of all, they are a percentile, so although they do make a comment on teachers relative to eachother, they don't actually comment at all on effectiveness of any teacher.
Secondly, because they compare one year's score to the next, they don't even really comment on how effective any one teacher is, but rather, how effective one teacher is to the teacher the year before. This means an above average teacher can be ranked as below average if the teacher that teaches one grade level lower is superb. This will work in reverse also.
It's a sad day for education and a sad day for logical thought.
Hi Harris, David, Cedar and Matthew,
Thanks for your comments.
It seems very clear that I failed to emphasize sufficiently the point that a discussion about interpreting error margins is a separate issue from the accuracy of the model itself. It’s ironic that I’ve discussed this issue in too many previous posts to count, but not in this one, where it was so clearly important, given the fact that the databases are being viewed by the public. So, I’m sorry about that.
That said, I would make three other related points. First, this issue cuts both ways: Just as accounting for error doesn’t imply accuracy in the educational sense, the large margins are not necessarily evidence that the models are useless, as some people have implied. Even if, hypothetically, value-added models were perfect, the estimates would still be highly imprecise using samples of 10-20 students.
Second, correct interpretation, a big part of which is sample size and the treatment of error, can actually mitigate (but not even close to eliminate) some of the inaccuracy stemming from systematic bias and other shortcomings in the models themselves.
Third, and most importantly, I’m horrified by the publication of these data, period. Yet my narrow focus on interpretation in this post is in part motivated by a kind of pragmatism about what’s going on outside the databases. While the loudest voices are busy arguing that value-added is either the magic ingredient to improving education or so inaccurate as to be absurd, the estimates are *already* being used – or will soon be used – in more than half of U.S. states, and that number is still growing. Like it or not, this is happening. And, in my view, the important details such as error margins – which is pretty basic, I think - are being largely ignored, sometimes in a flagrant manner. We may not all agree on whether these models have any role to play in policy (and I’m not personally opposed), but that argument will not help the tens of thousands of teachers who are already being evaluated.
Thanks again,
MD
P.S. Cedar – The manner in which I go about interpreting and explaining statistics is the least of my psychological issues.
Matthew,
Thanks for this breakdown! Hope you or others can also address issues of sample size (especially in schools with high student turnover), and of the quality/ methodology used to produce the ELA & math assessments themselves -- if teachers are being judged on their students' scores, someone outside the testing provider/ NYSED needs to ensure the tests are fair. However, if the test shielding that occurred in 2011 continues, there is no way for a truly independent observer to evaluate the validity of the assessment vehicles, which makes for a very precarious foundation of an already structurally questionable evaluation system...
Matt, I too thank you for the helpful, thoughtful, and
dare I say it, balanced, treatment of the error issues, and the responses add value as well. A couple of additional questions: What do you think of Aaron Pallas's suggestion about a way to handle error, i.e. for any teacher's score that nominally falls within a particular category, you give it that label only if the confidence limits give it a 90% (or pick your particular % criterion) chance of falling within that band; otherwise, you give it the next higher rating (unless the error range is so high that you go even higher :-) Of course, that doesn't really confront the arbitrary nature of the choice of bands for "low" "below average" "average" etc. or the educationally ambiguous meaning of those classifications, but it would at least be a further accommodation of the error problem. But on that - a question - I don't really understand how error is attributed to individual teachers' percentile scores - is it really individual? If so, gee - interesting ... maybe because of class size, number of years of data, or -- what? Which brings me to - the percentiles here are referenced to the distribution of the average value-added scores of their students, which are based on discrepancies of each student's actual score from their predicted scores, based on regressions involving prior year scores and a kitchen sink of other variables, including student, class, and school characteristics - right? Are the error bands derived from the error stemming from all those individual regressions as they are summed and averaged and the averages turned in to
percentiles compared to the distribution of other teachers' averages? Wow! And how do the statistics factor in the noise in the test scores themselves, particularly at anywhere beyond the middle of the test score distribution? The NYC DOE website does go a little way in recognizing the problem of the noise at the upper (and lower) ends, and maybe all the stuff they throw into the equations somehow takes this into account, but boy it looks like a Rube Goldberg operation. I suppose the short way of asking this is -- where do those 30 to 50 or more confidence intervals come from, and is there even more error (not to mention validity questions) hiding behind them? Just askin' Anyway, great work, Matt. Fritz
Oh, and I notice that the DOE bases the teacher's percentiles on the distributions of value added score averages for teachers with the "same" amount of experience, rather than all teachers. Maybe that is marginally a fairer comparison - but is it? The DOE
website seems to say they are moving to a different approach (or the state is?) but I have no clue what it
will be. Colorado style growth percentiles maybe? Have to keep an eye on them, and for sure, don't turn your back.