What Is A Standard Deviation?
Anyone who follows education policy debates might hear the term “standard deviation” fairly often. Most people have at least some idea of what it means, but I thought it might be useful to lay out a quick, (hopefully) clear explanation, since it’s useful for the proper interpretation of education data and research (as well as that in other fields).
Many outcomes or measures, such as height or blood pressure, assume what’s called a “normal distribution." Simply put, this means that such measures tend to cluster around the mean (or average), and taper off in both directions the further one moves away from the mean (due to its shape, this is often called a “bell curve”). In practice, and especially when samples are small, distributions are imperfect -- e.g., the bell is messy or a bit skewed to one side -- but in general, with many measures, there is clustering around the average.
Let’s use test scores as our example. Suppose we have a group of 1,000 students who take a test (scored 0-20). A simulated score distribution is presented in the figure below (called a "histogram").
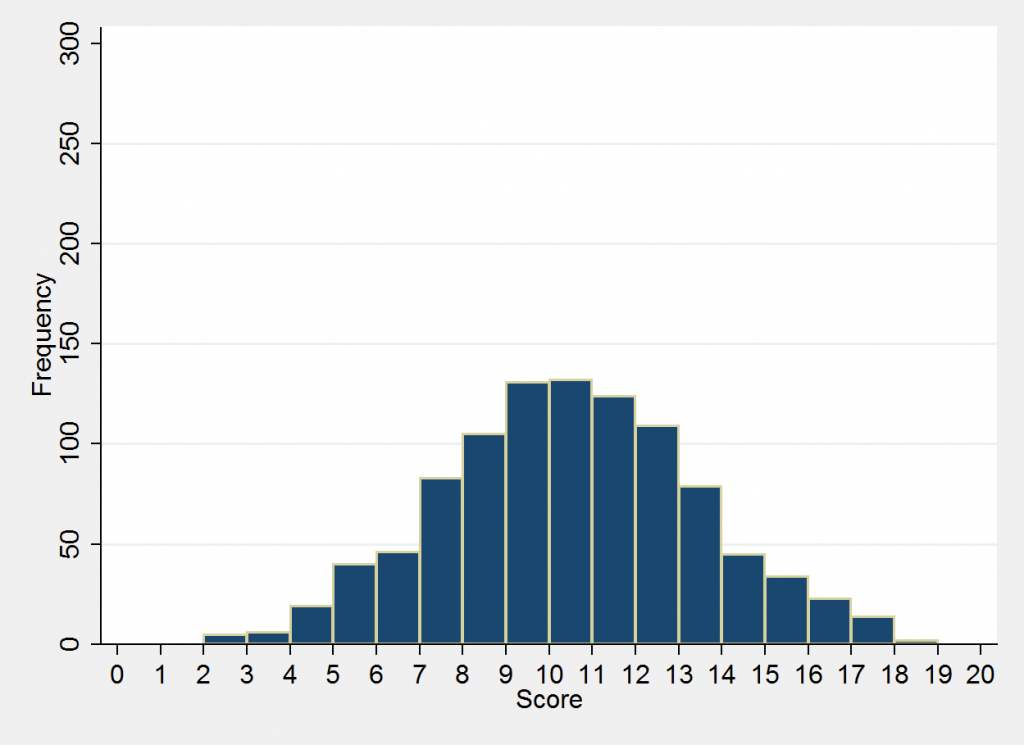
The numbers on the horizontal axis are test scores, from 0-20. The bars for each individual score tell you how many students received that score (frequencies are on the vertical axis). The bars for the scores around 10 (the average) are the highest, and they get shorter the further you move to the left of the right, since fewer and fewer students receive scores that are far away from the average.
Now look at the second graph, which is, let's say, the same test and number of students but a very different distribution.

In this case, the average score is still 10, but the distribution is much “tighter," with far fewer students scoring much higher or lower.
As you can see, the average score can be a useful summary statistic, but it can’t tell you about how students’ scores are actually distributed around that average. In the second graph, the scores are clustered fairly compactly, whereas in the first graph there is much more variation among scores. Two groups of students’ scores can have the same average but very different spreads.
Here’s where standard deviations come in. They are one way to measure this spread around the average. They are typically expressed in the same metric as the measure (in this case, test score points), and they are always a positive number. In general, the more variation there is from the average, or the less clustered are observations around the mean, the higher the standard deviation.
And this can matter. If, for example, these are two groups of students taking the same test, the two graphs present rather different pictures of how each set of students is performing. A teacher looking at the first graph might have to pay a bit more attention to differentiated instruction, as she is dealing with a wider spread of measured performance.
But what do the actual numbers mean? For instance, if we say that a given score is one standard deviation above the mean, what does that tell us?
Perhaps the easiest way to begin thinking about this is in terms of percentiles. Roughly speaking, in a normal distribution, a score that is 1 s.d. above the mean is equivalent to the 84th percentile.
On the flip side, a score that is one s.d. below the mean is equivalent to the 16th percentile (like the 84th percentile, this is 34 percentile points away from the mean/median, but in the opposite direction).
Thus, overall, in a normal distribution, this means that roughly two-thirds of all students (84-16 = 68) receive scores that fall within one standard deviation of the mean.
Moving further out into the tails of the curve, a score 2 s.d. above the mean is equivalent to a little lower than the 98th percentile, and 2 s.d. below the mean is equivalent to a little higher than the 2nd percentile. In other words, roughly 95 percent of students are within two standard deviations – positive or negative – of the average. (This, by the way, is the basis for the 95 percent confidence interval, of which you have no doubt heard.)
Now we can return to our graphs. In the first one, the standard deviation (which I simulated) is 3 points, which means that about two thirds of students scored between 7 and 13 (plus or minus 3 points from the average), and virtually all of them (95 percent) scored between 4 and 16 (plus or minus 6).
In the second graph, the standard deviation is 1.5 points, which, again, means that two-thirds of students scored between 8.5 and 11.5 (plus or minus one standard deviation of the mean), and the vast majority (95 percent) scored between 7 and 13 (two standard deviations).
As implied from these illustrations, each observation – or each of our 1,000 hypothetical students – can have their scores converted into standard deviations (called "z-scores"), and then we can (carefully) compare them to other scores – e.g., the same students’ scores on the next year’s test. Researchers often do this when test scores are not directly comparable between years or grades.
(Important side note: These conversions and comparisons are complicated and sometimes misleading. As just one illustration, only one or two additional correct answers might "move" a score quite a bit in terms of standard deviations on one test, but the same "move" might require several correct questions on another test. In this sense, normalizing scores might sometimes create the "illusion" of variation where there is actually relatively little.)
Just to keep it simple, let’s once again return to the two graphs above, and say they are the same group of students. The first graph, the one with the wider spread, represents their scores on the fourth grade exam, and the second graph represents their scores on the fifth grade exam. Thus, depending on the design of the test, a score of, say, 13 can’t be directly compared between tests. On the fourth grade test, for instance, a score of 13 is equivalent to the 84th percentile (one s.d. from the mean), whereas a score of 13 is at the 98th percentile in fifth grade (two s.d.). Obviously, these two raw scores aren’t telling you the same thing about a given student’s relative performance.
One might therefore actually convert the scores into standard deviations (this is called “normalizing"). Keeping our example of two scores of 13, in fourth grade this would be equivalent to a "z-score" of 1.0, since it is one standard deviation above the mean. In fifth grade, however, the equivalent conversion would be 2.0 (since it is two s.d. above the mean). The scores are essentially reconceptualized in terms of distance from the mean, so as to make them more comparable. This is one reason why you find research studies expressing estimated impacts (usually net of control variables) in terms of standard deviations - because the outcome variable is normalized.
Accordingly, let’s conclude with a brief discussion of how one might interpret educational research in which estimated impacts are expressed in standard deviations. Put simply, how can you tell if estimated effect sizes are meaningful?
That is complicated. There are no set rules for determining whether a given effect size is “large” or “small." It all depends on the outcome of interest, the type of intervention, the method of evaluation, the time frame (annual versus longer-term), and several other factors, including, of course, one’s expectations and subjective judgment (and remember that the term "significant effect" can be misleading, as discussed here).
In education policy, estimated effects are rarely larger than plus or minus one standard deviation, and most often they are somewhere between zero and plus or minus 0.5 standard deviations, or one-half of one standard deviation. But, again, this varies by context. In charter school studies, for instance, it’s unusual to find effects larger than 0.20-0.30 s.d., and most are between zero and 0.10 s.d. (one-tenth of one standard deviation). Other interventions, such as targeted reading improvement programs, curriculum, and certain early childhood programs, have in some cases yielded larger effect sizes.
In the interests of giving at least some rough idea, albeit one that is my personal approach, I tend to view estimated impacts of educational interventions that are lower than around 0.05 s.d. (five percent of a standard deviation) as small, and anything over 0.10-0.15 as substantial. Again, though, these are just very rough guidelines, and can vary quite a bit by context.**
To summarize, standard deviations are all about the spread of measured outcomes around the mean. In a normal distribution, values cluster around the mean and become less and less frequent as one moves to the left or right. This conceptualization can help you describe the spread of results, and it can also be used to (very cautiously and roughly) compare otherwise incomparable values. When the estimated impact of an interventions is expressed in terms of a standard deviation, interpreting it as “large” or “small” entails a lot of judgment and varies a great deal by context (e.g., type of policy). As such, it can be as much art as science, and that helps to explain at least some of our debates’ contentious nature.
- Matt Di Carlo
*****
* If you're interested, the standard deviation is the square root of the variance, which is the average of all observations' squared differences from the mean.
** As discussed above, you can also think about this in terms of percentile changes, but remember that a given effect, when expressed in standard deviations, "translates" into different percentile changes depending on where you're looking in the distribution. In other words, the increase (or decrease) in percentile varies depending on where you "start out." For instance, in a normal distribution, a jump of 0.5 s.d. (one half of one standard deviation) is equivalent to moving from the 50th to the 69th percentile, but it's also equivalent to the difference between the 84th and 93rd percentiles. Keep that in mind when you hear researchers express effects in this manner (see here for a good example).

Good stuff, Matt.
One of my great frustrations is how easily so much education research converts S.D.'s into some "real" measure that isn't "real" at all. "X months/years of learning" is a particularly popular one, but I would argue it distracts from the actual outcome, which is a change in the number of questions answered correctly on a test.
If I were king of Dataland, I would forbid this practice without, at the very least, first telling us what was really being converted into S.D.s -- in the case above, telling us how many questions on a test (or even raw score points) leads to a change from a z-score of 0 to 1.
Mark
Matt, Mark --
Can any of you comment on exactly what we're talking about when one teacher has a higher value add score than another?
For example, on a 65 question state multiple choice exam, does a "high performing" teacher get his/her students to get 57 questions correct, while a "low performing" will on average get his/her students to score....53 correct? 50? 40?
How many questions are we talking about? Of course it's different for different states and depends on the test, but can either of you give a general ballpark of what we're talking about here?
While I understand the approach of standardizing scores for research purposes, I agree with those who argue it's important to translate back the differences into # of additional questions answered correctly. This is particularly important in those states that use Student Growth Percentiles. Most people fail to appreciate that in the middle part of the distribution, where there are lots of students, a difference in 1 question answered correctly bumps the SGP up dramatically... And indeed there might be absolutely no difference between an SGP of say 45-55 in number of items answered correctly because say 10 percent of respondents have the median # of items answered correctly...
Matt,
Very interesting post. I think its really important to explain standard deviations to a non-statistical audience.
Two responses to your post and people's comments
1. Using standard deviations to compare between populations is a potentially risky endeavor. Since standard deviation is based on the variance, a mean difference in a population with less variance will seem to have a larger effect size than the same difference in a population with greater variance. So an intervention with a more homogenous population may seem to have a greater effect than a more diverse population.
2. There's no way to directly convert standard deviations into the number of correct responses. Most standardized tests don't use the raw percent correct to calculate scores. Rather, statistical models to estimate student scores based on their response patterns. So depending on what questions they answered correctly students will get different scores.