Revisiting The "5-10 Percent Solution"
In a post over a year ago, I discussed the common argument that dismissing the “bottom 5-10 percent" of teachers would increase U.S. test scores to the level of high-performing nations. This argument is based on a calculation by economist Eric Hanushek, which suggests that dismissing the lowest-scoring teachers based on their math value-added scores would, over a period of around ten years (when the first cohort of students would have gone through the schooling system without the “bottom” teachers), increase U.S. math scores dramatically – perhaps to the level of high-performing nations such as Canada or Finland.*
This argument is, to say the least, controversial, and it invokes the full spectrum of reactions. In my opinion, it's best seen as a policy-relevant illustration of the wide variation in test-based teacher effects, one that might suggest a potential of a course of action but can't really tell us how it will turn out in practice. To highlight this point, I want to take a look at one issue mentioned in that previous post – that is, how the instability of value-added scores over time (which Hanushek’s simulation doesn’t address directly) might affect the projected benefits of this type of intervention, and how this is turn might modulate one's view of the huge projected benefits.
One (admittedly crude) way to do this is to use the newly-released New York City value-added data, and look at 2010 outcomes for the “bottom 10 percent” of math teachers in 2009.
Before doing so, however, it bears making a couple of quick points. First, any discussion of the stability or estimation error of value-added scores is related to but cannot adequately address the question of whether they represent unbiased estimates of teachers’ causal effects on test score gains (though large error margins also don't mean the models are "wrong," as is often implied). That is, whether the models can account to an acceptable degree for all the factors, school and non-school, that are outside of teachers’ control. I am much more sanguine on this issue than other people (including many teachers), but it is a critical caveat that one must always keep in mind.
Second, virtually no one, including Eric Hanushek (who is a respected researcher), supports dismissing teachers based solely on test scores. His argument is that “true teacher quality” (which cannot be observed) probably varies as much as test-based effectiveness (i.e., value-added), and that teachers who produce high testing gains likely tend to be those who also compel student progress in other, less measurable areas. Thus, by simulating a policy based on value-added, we’re also, to some degree, simulating a policy based on more “holistic” measures of teacher productivity, and that policy's effect on more comprehensive student outcomes overall. More on this later.
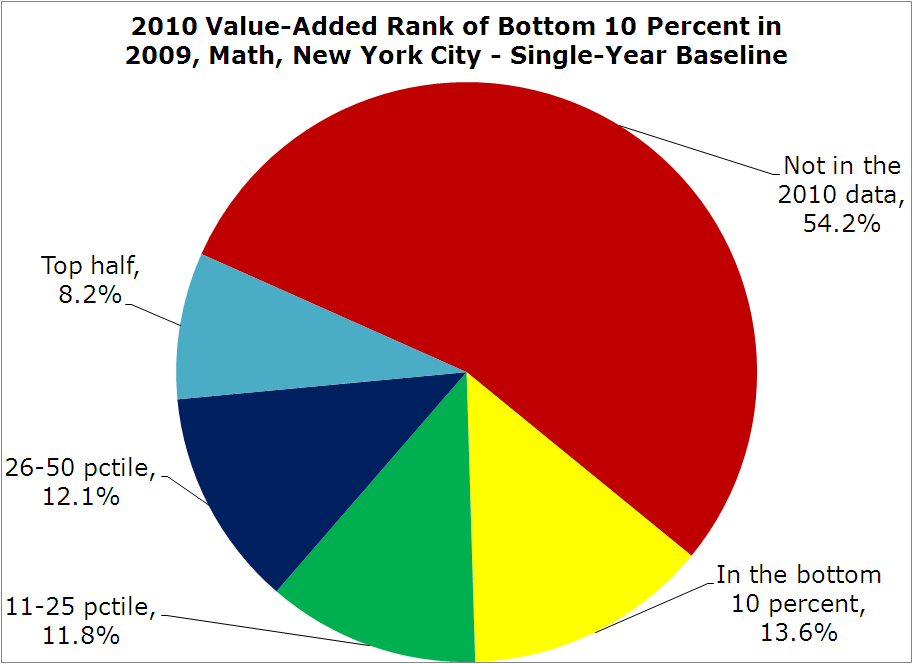
Moving, on, there are roughly 1,000 teachers with bottom-decile (“bottom 10 percent”) math value-added scores in 2009. Just to keep things as simple as possible, let’s see how they did in 2010 in terms of their percentile ranks (even though the ranks aren’t a great way to represent these data [addressed below] and the scores themselves, no matter how you present them, are imprecisely-estimated).
Over half of these 1,000 or so teachers were not in the 2010 data. They may have retired, resigned, switched districts, changed to a non-tested grade/subject or been dismissed (a few may have also had an insufficiently large sample of students to receive an estimate). So, it’s definitely worth noting that, at least in 2009 in New York City, half of the “bottom 10 percent” teachers were out of the sample by 2010, voluntarily or involuntarily, without a policy to remove them systematically. There seems to be a lot of deselection going on already (a quick and dirty logit model suggests that higher-value-added teachers are less likely to be gone from the dataset in 2010, which is consistent with the real research on this topic).
Among the remaining 500 or so teachers, 137 repeated their “performance," at least by value-added percentile rank standards – i.e., they were again ranked among the bottom 10 percent in 2010. A roughly equal proportion scored between the 11th and 25th percentiles, and between the 26th percentile and the median. Finally, 82 teachers (8.2 percent of all the bottom 10 percent teachers in 2009) actually ranked in the top half in 2010 (though, again, many of the estimates sorted into these categories are statistically indistinguishable from each other).
So, if these teachers were dismissed based on their 2009 rating – at least those who wouldn’t have “left” anyway – there was some spread in their 2010 results (in terms of percentile ranks), though they were still more likely to score in the bottom half of the distribution than the top.
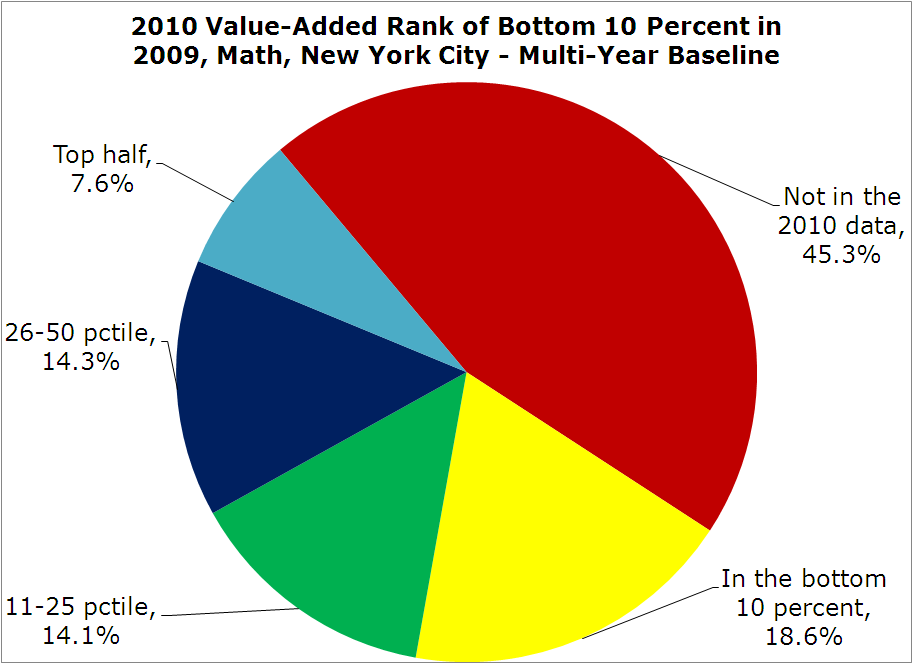
One might rightfully object that this simulation is not only crude, but it “dismisses” teachers based on their 2009 estimates alone. The more practical way to carry out this hypothetical policy would be to limit our focus to teachers who have multiple years of prior value-added scores. The reason would be that multiple-year estimates are less noisy, and are therefore better-able to predict how teachers score in 2010 (there is indeed a higher correlation between years using the multi-year baseline).
So, let’s repeat the same simple exercise, but this time only use teachers’ 2009 value-added scores that are based on multiple prior years between 2006 and 2009, with some of them having only two years of data and others having three or four. This means we’ll be looking at fewer teachers, since not all of them have multiple-year scores. We get roughly 500 teachers who scored in the lowest decile on their multi-year value-score (averaged over 2006-2009), and here’s how they did in 2010.
The rank stability is a little better, but not by much. A slightly lower proportion (45.3 percent) of these teachers were not in the 2010 data compared with the last graph, which makes sense, since these teachers would be, on average, more experienced (because they had to have at least two years of data), and would therefore be less likely to leave or be let go. Among those 279 teachers who “stayed” (i.e., had 2010 data), only 95 of them again ranked in the bottom 10 percent in 2010, while, once again, about twice as many ranked higher.
So, teachers who would have been dismissed in 2009 – even using multiple years of estimates – were again rather spread out in 2010.**
But using the ranks for this comparison, though easy to understand, is far from ideal. This is not only because ranks can be seriously misleading - e.g., they hide often trivial differences in underlying scores - but also because, when you have less data, as in 2010 compared with the 2009 multi-year estimates (averaged between 2006 and 2009), you’ll get a bigger spread of scores around the average.
For this reason, in 2010, the high scores are higher than in 2009, and the low scores are lower. As a result, the actual value-added score that separates the “bottom 10 percent” from the rest of teachers is different in 2009 compared with 2010. For example, the average value-added score of a 10th percentile teacher in 2009 (multi-year) is -0.16, compared with -0.26 in 2010 (single-year).
Insofar as we’re trying to see whether “bottom 10 percent” teachers in 2009 scored at a similarly low level in 2010, it matters that the ranks mean different things in both years.
One way to partially address this issue would be to look at teachers' multi-year estimates in 2009 (2006-2009), and then look at future outcomes that are also based on multiple years of data. I cannot do that with the NYC data, but an acceptable, easy-to-understand alternative might be to simply ignore the percentile ranks in 2010, and look at the actual scores of teachers who were in the “bottom 10 percent” in 2009.
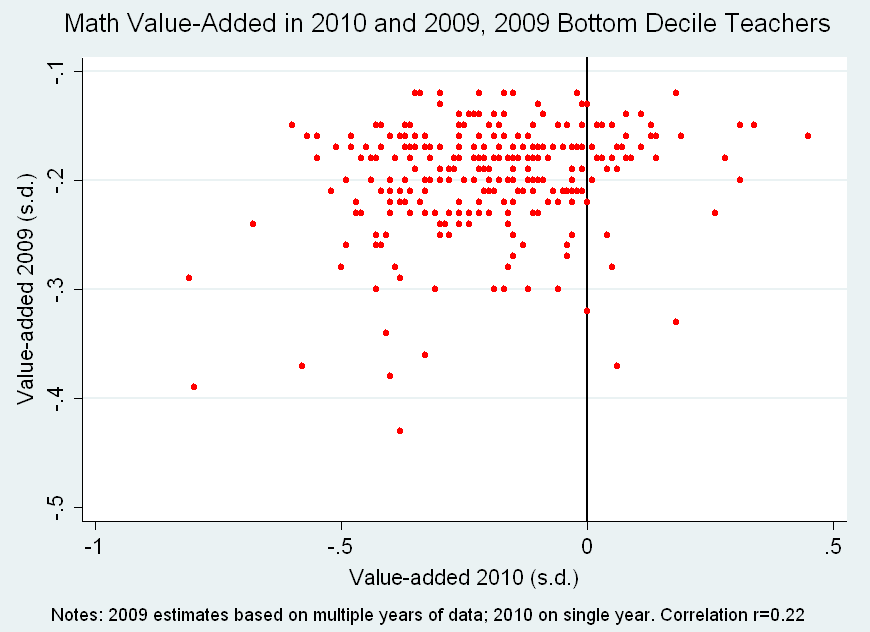
Take a look at the scatterplot below – each red dot is a teacher, and the dots include only those teachers in the lowest decile in 2009 (that’s why the vertical axis, which is the 2009 score, starts below zero). Note that the axes use very different scales.
From this perspective, using the percentile ranks in 2010 might somewhat overstate the degree of instability. Most of these teachers (but not all) did have a negative value-added score in 2010 (the horizontal axis), and a fairly large proportion of them (about two-thirds) are lower than the 2009 bottom decile cutoff point.
But the margins of error on the 2010 scores are also much, much wider, which means that we can have far less confidence that their “true” effects – at least as measured by these models – is where it’s estimated to be. Actually, in part because the 2010 estimates are based on one year of data, almost half of all these teachers' scores are statistically indistinguishable from the average (many quite similar to their presumed replacements), when you account for the imprecision of their estimates, and a bunch - about one in ten - have estimates (also imprecise) above the median (those to the right of the black vertical line in the middle of the graph).
Conversely, but not shown in the graph, among those teachers who scored above the bottom decile in 2009 (and thus would not be dismissed) but were still in the data in 2010, around one-quarter of them had value-added scores below the 2009 bottom decile cutoff point. These teachers, in addition to any new teachers scoring below the threshold, might also have to be dismissed to maintain anything resembling the full impact of the simulation. Ongoing deselection could result in some pretty severe turnover, even in the years following the initial wave of deselection, and would place further demands on the labor supply of replacements.
(One other fun fact: Among the roughly 3,400 teachers who have [single-year] math scores for each year between 2008 and 2011, about one in five ranked in the bottom decile in at least one of these three years, while only nine teachers ranked in the bottom 10 percent in all three [remember, however, that many bottom decile teachers leave the dataset].)
In short, then, even using scores based on multiple years of prior data, there is a great deal of diversity in the outcomes for these teachers in 2010.
These simple results are not at all a revelation – the imprecision of value-added estimates results in high instability between years. As a result, making decisions based on these estimates – or any other performance measure, for that matter – means you’ll be rewarding or punishing many teachers who will score quite differently the next year.
This is consistent with not only the broad literature on this topic (also here), but also one of the findings from the recent, much-discussed Chetty/Friedman/Rockoff paper on the long-term effects of teachers. They carried out the least "aggressive" version of the Hanushek simulation – deselecting teachers with the lowest five percent of scores – using real data over time (also from NYC, but in a much more thorough fashion, and looking at long-term student outcomes, rather than just 2010 results).
One of the findings from this replication, which was barely mentioned, was that, due to random error, the projected “benefits” of deselection based on one year of data (averaged across math and reading) are reduced by 50 percent (relative to deselection on “true” value-added), and reduced by 30 percent using three years of data. (Note that these decreases are relative to their own projections, not Hanushek's.)
Put simply, even if you assume that value-added estimates are adequate approximations of teachers’ causal effects, they are so error-prone, even toward the tails of the distribution, that simple random noise will severely mitigate the projected benefits of any decisions based on these estimates (the situation is even worse in English Language Arts). And insofar as the noise (and other issues, such as replacements, turnover, etc.) will be a factor in any real world approximation of this policy, the simulation, taken at face value, is making promises that it cannot keep.
***
Does this mean that there’s no way to identify low-performing teachers? Or that poorly performing teachers who can’t be helped to improve shouldn’t be dismissed? Of course not.
By any measure, putting aside whether these estimates represent relatively unbiased causal effects, the “bottom 10 percent” of teachers in 2009 scored much lower in 2010, on average, than teachers who were above the “bottom 10 percent” in 2009. The relationship is imperfect, but it's there.
However, ask yourself: If we cannot use value-added scores alone to zero in on low-performing math teachers, and we can’t say with much confidence what their test-based “effects” will be in any given year based on those in previous years, then what does it mean to say that dismissing the bottom 5-10 percent of teachers based on value-added alone would raise U.S. performance to the level of high-performing nations? What does this tell us about real world policy?
Look, it’s plausible to believe that “true teacher quality” (which we cannot observe) varies as widely as do value-added scores, even if the latter cannot be used exclusively to approximate the former. It’s also reasonable to argue that a thoughtful, well-designed evaluation system might do a decent job of measuring that “true quality," that value-added scores will be at least modestly correlated with the non-test-based components of those evaluations, and that, if all goes well, there would be improvement overall, perhaps impressive improvement in the long-term, were teachers who consistently scored poorly to either improve or be let go (though, again, many leave anyway).
If that was all that anyone took away from the “5-10 percent” calculation, then there would be no objection, at least not from me.
But the power of the simulation is not in its demonstration that teachers matter, or that there are big differences between low-performing and average teachers’ estimated impacts on test scores. It’s not because it shows that good teachers should be identified and cultivated, that there are poorly performing teachers who should be dismissed or that doing so would improve overall performance, at least to some degree. Most everyone knows these things (though it’s useful to illustrate them empirically).
Rather, the appeal of the simulation is in the size of the benefits it promises – for many people, it says that all we need to do is start terminating these “bottom” teachers, and within a relatively short time frame, results will improve so dramatically that they would, if replicated nationally, place U.S. scores among the best in the world. One large-scale intervention, and all is well.
If one wants to argue that the actual benefits from a more feasible policy of this sort – i.e., one based on good evaluations – need only be a small fraction of those estimated by the “5-10 percent” calculation to be worthwhile, that's fine. So too is asserting that the calculation illustrates the potential benefits of improving/removing persistently low-performing teachers.
But these are very different statements from saying that deselection by itself can raise scores to the top international levels in a decade or so. It’s the difference between realistic and unrealistic expectations, and many people seem to have latched on to the unrealistic end of this equation. Obviously, Hanushek's calculation didn't cause this situation but, when interpreted (incorrectly, in my view) as a projection of benefits from a concrete policy evaluation, it fuels the fire.
Expectations matter. Pundits and policymakers have become fixated on “firing bad teachers," rather than also improving all teachers and the environments in which they work (Hanushek's preference is actually for the improvement course, but he's skeptical about the potential for success of such efforts).
In addition, the relentless, at-all-costs effort to begin systematic dismissals more often than not ends up giving short shrift to all the critical details that determine success or failure in policymaking, including, in this case, the essential first steps of rigorously measuring teacher quality (to the degree possible), figuring out how to use this information in effective personnel decisions, allowing for at least a year or two of field testing and paying close attention to monitoring the effects.
Finally, after implementation, instead of maintaining realistic expectations - slow, steady improvements over a period of many years - people will expect the miracle. When the anticipated results fail to show up, annual testing data will become even more politicized, while opponents will call for an end to programs that might actually be working but haven't been given enough time.
The issue of low-performing teachers is serious and must be addressed with seriousness. That’s all the more reason not to rush to implementation of real world policies, and to keep an extremely level head about the size and speed of any one policy's impact.
- Matt Di Carlo
*****
* Simplifying things a bit, the calculation is based on a large dismissal of the “bottom 5-10 percent” in year one, not, as is sometimes claimed, a policy that fires a specified percentage every year. Within the simulation, however, dismissals would have to be “maintained” in subsequent years were any new teachers to score below the “bottom” threshold, while the replacement teachers are assumed to have average value-added scores. In other words, the simulation basically assumes that, after the first year, there no longer any non-novice teachers whose value-added scores are below the original dismissal threshold - i.e., that we can identify the "bottom" teachers going forward, based on previous estimates.
** We might take this one step further and say we only dismissed teachers in 2009 who were ranked in the bottom 10 percent, but included only teachers who had four full years of data (165 teachers). As expected, doing so improves the stability, but not by much. Only about one-third were “gone” by 2010 (which makes sense, since they’re more experienced, and thus less likely to turn over). Among the 109 remaining teachers, 42 of them scored in the bottom 10 percent in 2010 (one-quarter of all the teachers, including those who “left”). A slightly higher number (55) scored above the bottom decile but below the median, while around a dozen scored in the top half. Chetty/Friedman/Rockoff (discussed above) estimate that the marginal returns to using additional years of data level off after about three years, which suggests that expanding the relatively short time frame of the NYC data (a few years) may not help much.

The Report argues that economically it is better to fire a low Value Added teacher even after limited data and replace him/her with an average VA teacher.
Replacing a poor teacher with an average one would raise a single classroom’s lifetime earnings by about $266,000, the economists estimate. Multiply that by a career’s worth of classrooms.
Chetty/Friedman/Rockoff paper
You can't dismiss it when it uses 20 years of data.
I think it is important to note the following realities:
1. The tests to measure "value" are not worth the paper they are printed on. Reliability, validity, and relevance are absent. They do not measure what K-12 should be achieving.
2. Good teachers does not equal high test scores, or high 1-year increases.
3. We are talking about humans and learning, which are not linear or 2-dimensional or steady. They are complex and erratic, which is not accounted for when treated in a linear statistical model.
4. The language of "good teacher" and "bad teacher" based on test scores is offensive, new, simplistic, and toborrow from Sports Illustrated, a "Sign that the Apocalypse" is upon us, educationally-speaking.
5. Finally, it is sad. We know good assessment, good teaching, and what kids need to be successful(in every sense of the word) as adults. We prefer the fast, cheap, simple, numerical with a strong dose of scapegoating.
It's curious in reading the link from "calculation" to the paper by Hanushek that no where in the paper did a calculation appear. We're supposed to believe his conclusions based on his suggestion and his prior work (though it did mention the Gary, Indiana study). It really would have been nice to see the data that would support the reasonableness of his assumptions such as how a difference in teacher effectiveness based on test scores translated to a consistent response of student learning. Instead he gives an estimate and then goes on to say that estimate is a likely lower bound. Unfortunately, we are left with if you assume this and you assume that some students might have astounding gains while others will be permanently damaged.
As you have clearly shown, it's difficult to demonstrate any reliability in the these VAM scores and a supporter of using VAM scores is left to arm wave that they are still useful. Unfortunately,reformers believe in VAMs despite the lack of reliability because they see the alternative as no accountability. As mentioned just this last weekend on Up With Chris Hayes, 99% of all teachers (supposedly) receive satisfactory ratings making current non VAM evaluations meaningless. If you're starting point is that teachers (or administrators) can't be trusted, even unreliable VAMs will be seen as an improvement.
You suggest that "value-added scores will be at least modestly correlated with the non-test-based components of those evaluations". It's not clear what that would mean in practice. If there is not a great deal of variation in the non-test-based components for a number of teachers, but there is significant variation in the test-based scores, the test-based component of their evaluation is likely to dominate the evaluations. Add to this the possibility the value-added scores might be viewed as the only "objective" portion of the evaluation, these scores could end up being given more weight regardless of the actual legislation.
As you say, "Expectations matter", but so do the assumptions of those policy makers. If your assumption is, irrespective of factors beyond a teacher's control, teachers are effective or they're not, that a poorly performing teacher in one setting might not become an effective teacher in another, that poorly performing teachers can't improve, or that you can reliably replace your dismissed teachers with ones that are at least average all the time your policies are just as likely do more damage than lead to these hoped for huge improvements. Just what should our expectations be if those 5-10 percent all happen to teach in the same schools.If you already allow there is a concern about the distribution of quality teachers in a district, will this policy improve this situation or make it worse (in practice, not just in theory?)