When Growth Isn't Really Growth, Part Two

Last year, we published a post that included a very simple graphical illustration of what changes in cross-sectional proficiency rates or scores actually tell us about schools’ test-based effectiveness (basically nothing).

In reality, year-to-year changes in cross-sectional average rates or scores may reflect "real" improvement, at least to some degree, but, especially when measured at the school- or grade-level, they tend to be mostly error/imprecision (e.g., changes in the composition of the samples taking the test, measurement error and serious issues with converting scores to rates using cutpoints). This is why changes in scores often conflict with more rigorous indicators that employ longitudinal data.

In the aforementioned post, however, I wanted to show what the changes meant even if most of these issues disappeared magically. In this one, I would like to extend this very simple illustration, as doing so will hopefully help shed a bit more light on the common (though mistaken) assumption that effective schools or policies should generate perpetual rate/score increases.

Let’s first quickly review the illustration presented in the previous post, which is pasted below.

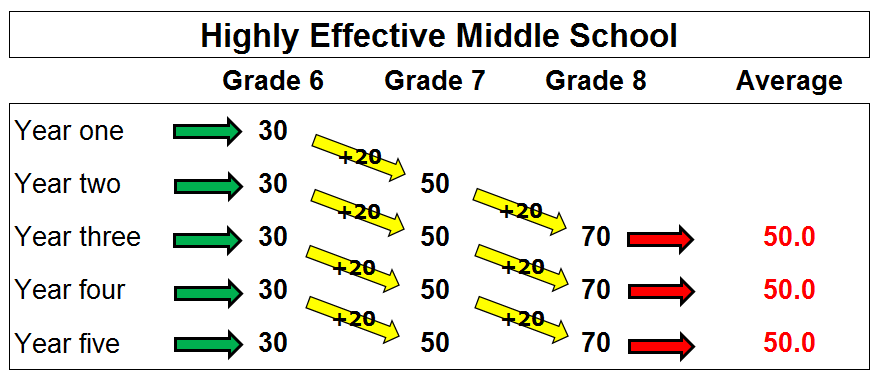
Here we have a hypothetical progress of test scores in a highly effective middle school. In this school, we have applied our magical assumptions, which basically eliminate the normal sources of volatility/imprecision that plague these cross-sectional changes in real life:

We are using actual scores instead of proficiency rates (read this great paper about problems with the latter);
Every single incoming cohort of sixth graders is the exact same size and performs at exactly the same level as their predecessors (with an average score of 30);
There is no mobility at this school – the same students who enter in sixth grade attend the school for three years. None of them leaves and no new students arrive.

As you can see, our middle school is wonderfully effective. Every year, each student picks up 20 points on the test. They go on to high school with an average score of 70. Notice, however, that the average score of the school does not change.

This is because we are not following the same group of students over time. Every year, the eighth graders leave the school at their highest performance level and are replaced by a cohort of sixth graders at the lower level. No matter how many tested grades in a school, and even if the growth rate varies between grades, the schoolwide average will not change. So, by the highly flawed standards that dominate our education discourse and federal policy, this incredible school would likely be judged a failure because its average performance is low and is not increasing. It would be seen as not showing growth, even though its students' scores grow by huge amounts every year.

This shows you the ridiculousness of interpreting cross-sectional score/rate increases as measures of school performance. Even in impossibly ideal circumstances (no change due to mobility, no differences between cohorts, etc.), they do not actually tell us anything about a school's effectiveness in a given year.

Now, what might they tell us? In other words, what (besides error/imprecision, which we have assumed away) might cause an increase in average scores?

This would require a year-to-year change in growth rates (even if just for one grade). For instance, let’s assume that some effective intervention did in fact lead to an immediate, one-time increase in this school’s effectiveness – instead of a +20 annual growth rate, the policy increased the average annual test score jump to +30.

To illustrate what would happen, let’s recreate the graph with the original +20 effect in years one and two (indicated by the yellow arrows), but increase that impact to +30 in year three (the first year of the intervention). The new effect is indicated by the blue arrows.

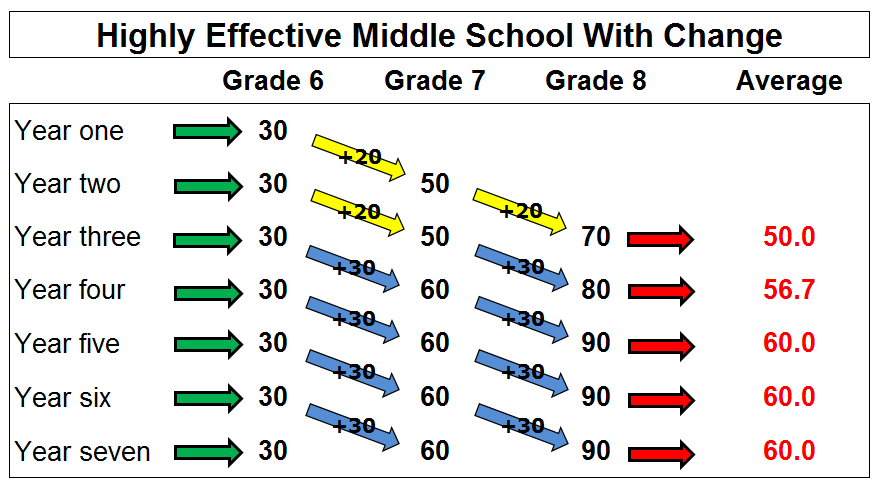
You can see that the school’s average score increases from 50 to 56.7 in the intervention’s first year, and then from 56.7 to 60 in the second year. After that, it levels off again.

What this tells you is that cross-sectional score/rate increases, even when we assume away imprecision, don’t tell you anything about schools' (test-based) effectiveness, but rather about changes in that effectiveness. When the school’s growth rate increased from +20 to +30 due to the intervention, there was a jump in the average score for a couple of years. Importantly, however, it leveled off as students who experienced the change midstream cycled out of the school.

Obviously, this is all purely illustrative. In the real world, the gains from beneficial policies often take a while to become measurable, vary widely by grade, student, etc. And, one last time - we have assumed away the big drivers of changes for the purposes of this illustration.

Still, the point here is that even a wonderfully effective policy may not generate a long period of increasing cross-sectional rates/scores. The policy impact would theoretically only manifest itself so long as it was improving the school’s average rate of test score growth (with a lag). Some policies might unfold over long periods, but many might not. And, in either case, it is the growth rate that matters here, and it doesn't always manifest itself in schoolwide scores/rates in an intuitive manner. There is certainly something to be said for expecting schools to avoid complacency and keep trying to improve, but it's also important to understand how that improvement can be monitored.

- Matt Di Carlo

Blog Topics