The Structural Curve In Indiana's New School Grading System
The State of Indiana has received a great deal of attention for its education reform efforts, and they recently announced the details, as well as the first round of results, of their new "A-F" school grading system. As in many other states, for elementary and middle schools, the grades are based entirely on math and reading test scores.
It is probably the most rudimentary scoring system I've seen yet - almost painfully so. Such simplicity carries both potential advantages (easier for stakeholders to understand) and disadvantages (school performance is complex and not always amenable to rudimentary calculation).
In addition, unlike the other systems that I have reviewed here, this one does not rely on explicit “weights," (i.e., specific percentages are not assigned to each component). Rather, there’s a rubric that combines absolute performance (passage rates) and proportions drawn from growth models (a few other states use similar schemes, but I haven't reviewed any of them).
On the whole, though, it's a somewhat simplistic variation on the general approach most other states are taking -- but with a few twists.
For elementary and middle schools, on which I will focus in this post, the grades are calculated as follows, with all steps except the last one proceeding for math and reading separately (schools can also lose points for low participation rates, but this is most likely relatively rare):
- Each school is assigned a “baseline” point total between 0-4, based on its passing rate (the scoring categories are listed in the first footnote).*
- The baseline scores are then adjusted using the following three “growth” outcomes (cutoffs listed below are for reading; they’re slightly different in math):
- If more than 42.5 percent of their lowest scoring quartile (lowest 25 percent) of students show “high growth," they gain one point (they cannot lose a point);
- If more than 36.2 percent of their highest scoring quartile (highest 25 percent) of students show “high growth," they gain one point (again, they cannot lose a point);
- If more than 39.8 percent of all students show “low growth," they lose one point (they cannot gain a point).
- The average of the final point totals in math and reading is the school’s final “GPA," which is then assigned a grade.
Let’s try to briefly address the important question of what these grades might be telling us about school versus student performance.
A quick review of what I mean by that distinction: In describing these systems, I usually focus on the relative role of absolute performance (how highly students score) versus growth (how quickly students improve). The former type of measure, usually gauged with proficiency rates, tells you more about student performance than school performance. Even the highest-performing schools – those compelling strong gains from students – might be poorly rated based on absolute performance, due to little more than the students they are assigned (and/or error). Growth models, on the other hand, when properly interpreted, can potentially do the opposite (albeit imperfectly and imprecisely), since they're designed to isolate school effects while controlling for factors that are out of schools' control.
Most school rating systems capture both school and student performance (and they are of course interrelated). States have an interest in gauging both, but it’s critical that they distinguish between them and calibrate interventions accordingly (see here for more on these measurement issues, and here for a discussion of how accountability systems are as much about incentives as "accuracy").
One easy way to illustrate the degree to which ratings – or any individual component - are capturing student rather than school performance is to see if they are associated with important demographic characteristics, such as poverty. The mere presence of an association doesn’t necessarily mean the ratings are “biased” or invalid, but it can help provide a sense of what they are telling you.
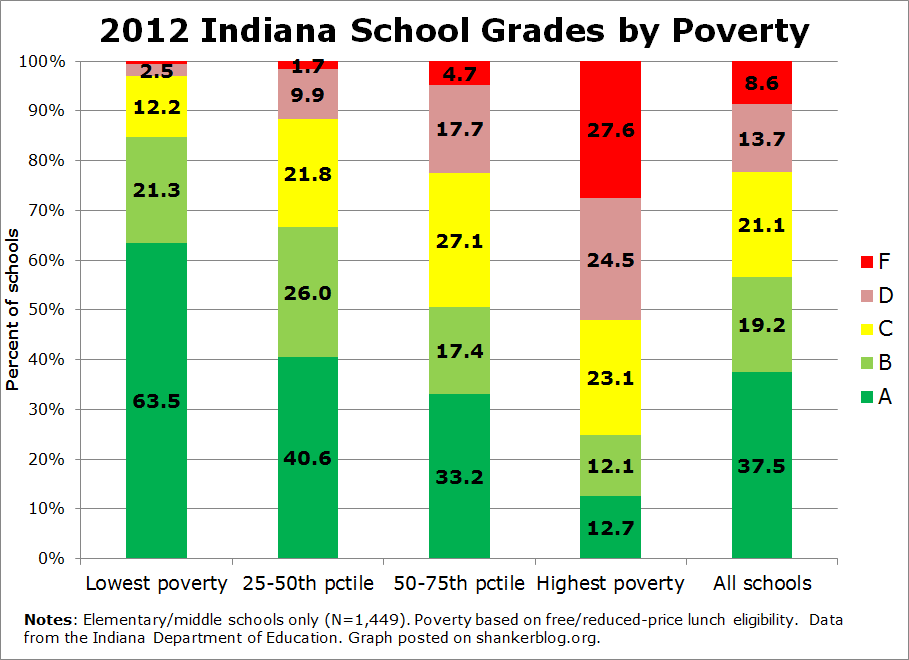
The simple graph below presents the distribution of grades for schools sorted into poverty quartiles, with poverty defined in terms of free/reduced-price lunch rates. I limit the sample to elementary/middle schools (the sample is 1,449 schools).
There's a very clear relationship here. Almost 85 percent of the schools with the lowest poverty rates receive an A or B, and virtually none gets a D or F. But the relationship is most visible among the poorest schools, a little over half of which are assigned an F or D, compared with about 22 percent across all schools. Actually, of the 125 elementary/middle schools that got an F this year, 100 were in the highest poverty quartile. Only eight were in one of the two lowest-poverty quartiles.
And just 25 percent of the poorest schools got an A or B, compared with almost 60 percent overall.
This is not at all surprising. It is baked into this system (and you'll see roughly the same thing in other states). Baseline scores are determined by absolute student performance (passing rates), which are heavily associated with student demographics such as poverty. As a result, final ratings vary systematically by poverty rates.**
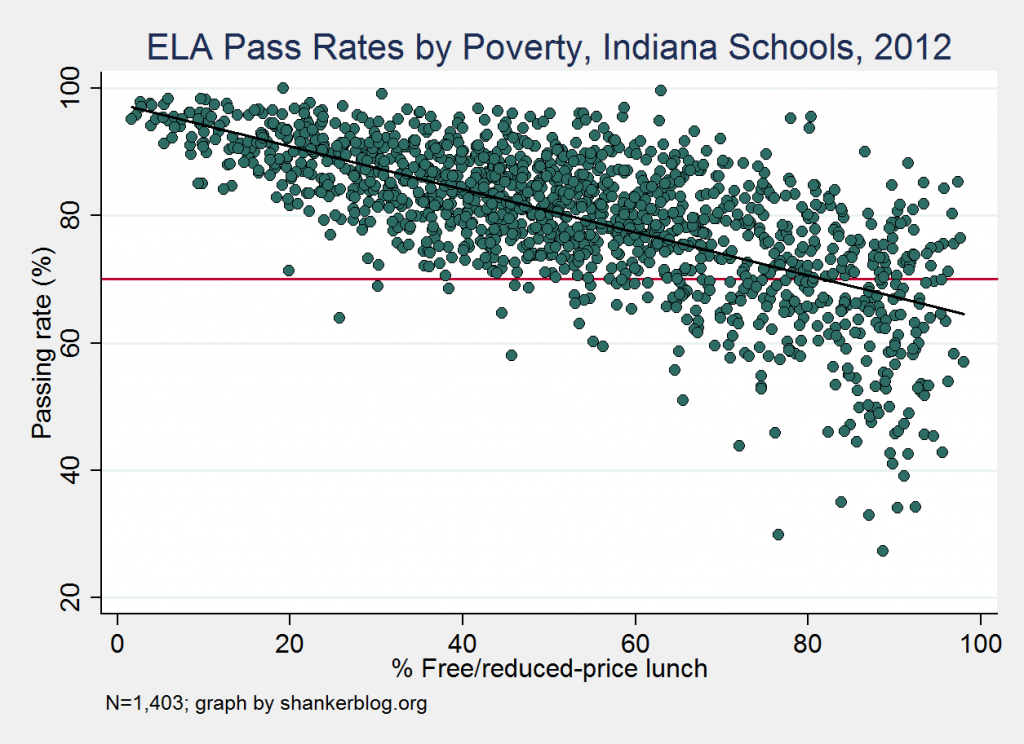
Another useful way to look at this is to use Indiana's simple rubric to calculate the minimum passing rate required for schools to have any mathematical shot at getting an A or an F (assuming they don't lose any points for low participation rates).
The magic number, if you will, is 70 percent. Any school with a passing rate of 70 percent or higher in both math and reading cannot receive an F no matter what (again, assuming they meet participation requirements). Conversely, any school with a passing rate below 70 has no mathematical chance of getting an A. Even if they get perfect growth scores (+2 net), the best they can do is a B.
About one in five elementary/middle schools - almost 300 in total - is in the latter situation – i.e., they have math and/or reading passing rates below 70 percent, and no shot at an A. Virtually all of these schools (95 percent) have poverty rates that are higher than the median. Three out of four are in the highest-poverty quartile.***
You can see this in the scatterplot below, which presents passing rates (in reading only) by school poverty, with the red horizontal line representing the 70 percent cutoff. Almost none of the schools below the line have free/reduced-price lunch rates lower than 50 percent.
On the flip side of this coin, the schools with rates above 70 percent (above the red line), some of which are higher-poverty schools, have no risk of a failing final grade, even if they receive the lowest possible growth scores. A grade of D is the floor for them.
So, it's true that even the schools with the lowest pass rates have a shot at a C, so long as they get the maximum net growth adjustment, and also that the schools with the highest passing rates might very well get a lackluster final grade (a C, if they tank on the growth component).
However, the most significant grades in any accountability system are at the extremes (in this case, A and F), as these are the ratings to which policy consequences (or rewards) are usually attached.
And, under Indiana’s system, a huge chunk of schools, most of which serve advantaged student populations, literally face no risk of getting an F, while almost one in five schools, virtually every one of which with a relatively high poverty rate, has no shot at an A grade, no matter how effective they might be. And, to reiterate, this is a feature of the system, not a bug – any rating scheme that relies heavily on absolute performance will generate ratings that are strongly associated with student characteristics like poverty. It’s just a matter of degree.
Finally, there are three other features of this system worth discussing quickly.
- First, Indiana’s reliance on binary “yes/no” coding at each nested level of aggregation (students, schools) sacrifices a lot of data, probably even more than is usually the case in these systems. As a result, for example, a school in which 50 percent of the lowest-scoring students show strong growth in reading gets the same reward (+1) as a school in which 100 percent are high growth. This means that the system, like proficiency rates, is very sensitive to where all those bars are set. The ratings might very well change a great deal with just minor adjustments in these cutoff points, and there will be a great deal more instability in ratings between years for schools that are located close to them.****
- A second feature of Indiana's system that bears mentioning is the fact that there is, in a sense, equal “focus” on the highest- and lowest-scoring students. Many states award points for growth among lower-scoring students (e.g., Colorado), but I hadn’t yet seen any doing so for high-scoring students. To be clear, I’m not at all saying this is a bad idea, only that it is unusual, and doesn't quite square with the (in my view, often oversimplified) national focus on narrowing achievement gaps.
- On a third, final and related note, you’ll notice that this system does not explicitly break down student performance by demographic characteristics, such as race or income. The subgroups are defined entirely in terms of prior scores (high- or low-scoring students). States that make this decision (Florida is another example) will still be held accountable for the performance of these subgroups by the federal accountability targets (AMOs), which makes for an interesting relationship between the state-specific and federal systems.
- Matt Di Carlo
*****
* Here is the breakdown of point totals by proficiency rate (decimals round down): 0-59=0 points; 60-64=1 point; 65-69=1.5; 70-74=2; 75-79=2.5; 80-84=3; 85-89=3.5; 90 or above=4.
** In addition, while I don’t have the data for Indiana, the type of growth model that they use also tends to be moderately associated with poverty, though much less so (see our post on Colorado).
*** The vast majority of the schools meeting this criterion are in the highest-poverty group, but, as you can see in the scatterplot above, the opposite is not true. Two out of five of the school in the highest-poverty quartile score above 70 percent in math and reading.
**** In assigning growth adjustment points, in addition to the models themselves (which convert scores to percentiles), there is data loss from dichotomization at the student and school levels: First, students are coded as showing "high growth/not high growth" or "low growth/not low growth"; second, schools are awarded or subtracted a point based on whether or not they're above the thresholds for those adjustments. The state doesn’t provide the data for each component separately, but the majority of schools are probably within a stone’s throw of the cutoff points, on either side (that might actually be how they’re determined). The fact that minor adjustments in the cutpoints might generate different results is often true when sorting scores into categories (including proficiency rates), but it may be particularly acute in this case.

Here is a song about the current education situation in Indiana. Please share.
http://www.youtube.com/watch?feature=player_detailpage&v=JfrKDoeG_Gk
If this link doesn't work do a youtube search for "Public School Fight Song (Indiana Version)".