Under The Hood Of School Rating Systems
Recent events in Indiana and Florida have resulted in a great deal of attention to the new school rating systems that over 25 states are using to evaluate the performance of schools, often attaching high-stakes consequences and rewards to the results. We have published reviews of several states' systems here over the past couple of years (see our posts on the systems in Florida, Indiana, Colorado, New York City and Ohio, for example).
Virtually all of these systems rely heavily, if not entirely, on standardized test results, most commonly by combining two general types of test-based measures: absolute performance (or status) measures, or how highly students score on tests (e.g., proficiency rates); and growth measures, or how quickly students make progress (e.g., value-added scores). As discussed in previous posts, absolute performance measures are best seen as gauges of student performance, since they can’t account for the fact that students enter the schooling system at vastly different levels, whereas growth-oriented indicators can be viewed as more appropriate in attempts to gauge school performance per se, as they seek (albeit imperfectly) to control for students’ starting points (and other characteristics that are known to influence achievement levels) in order to isolate the impact of schools on testing performance.*
One interesting aspect of this distinction, which we have not discussed thoroughly here, is the idea/possibility that these two measures are “in conflict." Let me explain what I mean by that.
Proficiency rates, though a crude and potentially distorted way to measure performance in any given year, tell you how highly students in a given school score on a test (or, more accurately, the proportion of students who score above a selected cut score). What most growth models do, in contrast, is estimate schools’ impact on testing progress while controlling for how highly students score (and, in some cases, other characteristics, such as subsidized lunch eligibility or special education).
In other words, growth models “purge” absolute performance levels from the data to help address bias. Students who start the year at different levels tend to make progress at different rates, and since schools cannot control the students they serve, growth models partially level the proverbial playing field by controlling for absolute performance (prior achievement), which is a fairly efficient, effective proxy for many characteristics, measurable and unmeasurable, that influence testing performance.
You can see this in the scatterplot below, which presents math growth scores (“median growth percentiles”) by proficiency for Colorado’s elementary and middle schools in 2011.
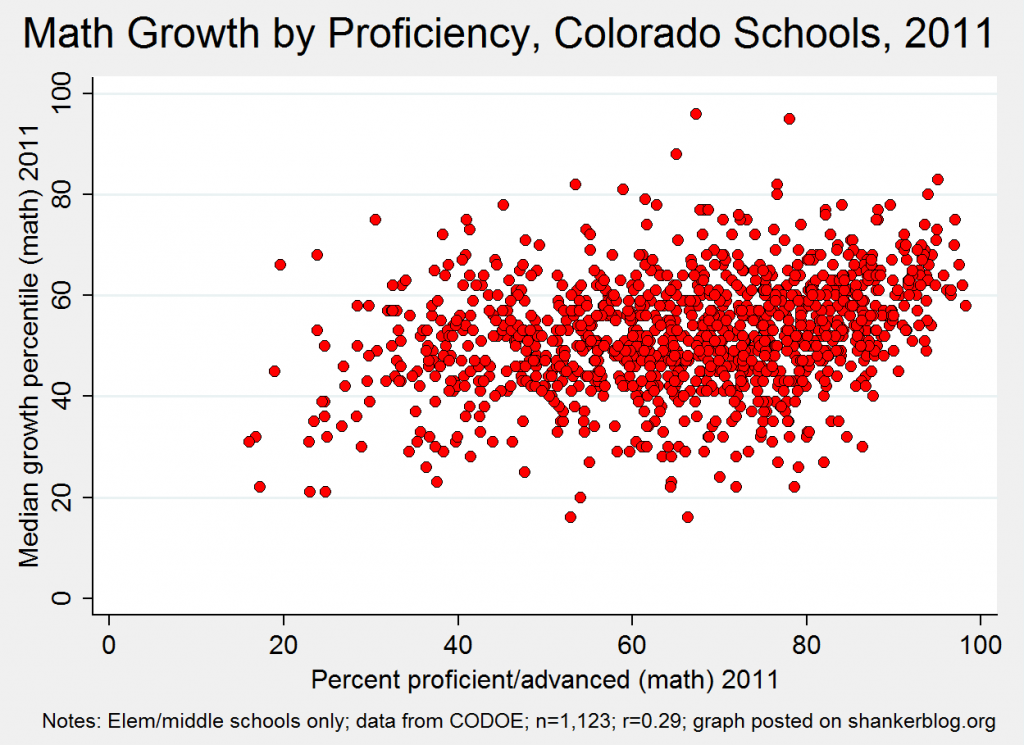
The association between growth scores and proficiency is modest at best, as is evident in the messy pattern of the dots in the scatterplot (and it is even messier when using many value-added models, as growth percentile models as commonly specified in accountability systems tend to exhibit a stronger relationship with student characteristics). In other words, in Colorado and elsewhere, many schools with high proficiency rates receive low growth scores, and vice-versa. This is in part because the latter controls for the former.
So, why are states’ rating systems combining two indicators, one of which (growth measures) is designed to "purge" the other (absolute performance) from the data? Put differently, if controlling for absolute performance is a key feature of growth models, why is it combined with those growth scores in most states’ school rating systems?
The answer, of course, is that these two general types of measures are not in conflict. They are simply measuring different things, both of which can be useful for accountability purposes. If, for example, you’re trying to target resources at students most in need of improvement, absolute performance measures can be an effective tool, as they tell you which schools are serving the largest proportions of these students. Parents might also find status indicators useful when choosing schools, as they have an interest in having their children attend schools with higher-performing peer groups.
If, on the other hand, you’re looking to implement more fundamental, higher-stakes interventions, such as so-called turnarounds, your best bet is probably to rely on growth measures, since they are designed to isolate (again, imperfectly) school effectiveness per se. You shouldn’t want to radically restructure a school that is compelling strong growth from its students, even if those students still score lower than their peers elsewhere.
(Side note: It also bears mentioning that the central purpose of accountability systems is to compel changes in behavior [e.g., effort, innovation], and it’s possible that these systems could have a positive impact, even if they employ exceedingly crude or “inaccurate” measures.)
The crucial distinction between what these two types of measures are telling us is why I and numerous others have argued that assigning a single rating to schools is inappropriate, and that there should be different ratings or measures employed, depending on the purposes for which they’re being used (also check out this idea for a similar approach).
In addition to the obvious long-term need to develop additional measures that go beyond state math and reading tests, this calibration of measures and how they're used is arguably the most important issue that must be addressed if these systems are going to play a productive long-term role in education policy.
- Matt Di Carlo
*****
* It bears mentioning that some states use growth measures in a manner that incorporates absolute performance, whether directly (e.g., Florida's growth indicator codes students as "making gains" if they remain proficiency in consecutive years) or indirectly (e.g., Colorado scores their growth percentiles partially by accounting for how far schools are from absolute targets). On a separate note, many of the newer systems also include measures focused on subgroups. In most cases, these indicators are simply growth scores for particular subgroups- e.g., Indiana places special emphasis on the "gains" among schools' highest- and lowest-scoring students. There are also, however, a few states, such as Ohio, that assess directly the extent to which score/rate gaps between various subgroups (e.g., FRL versus non-FRL students) narrow over time.

Matt,
Can you find a scattergram FOR A SINGLE URBAN DISTRICT, as opposed to an entire state, that looks that way? I'm afraid you've made the common mistake of value-added advocates who look at averages and entire states and thus miss the point. What would a scattergram of Denver look like?
Here's why this is important. Value-added can't adequately account for peer effects. Urban districts have suffered from decades of suburban flight, leaving concentrations of poverty and trauma. When you devise a target for a teacher, scores from the entire district, including those with positive learning climates like magnets and lower poverty schools are included and they create a target that tends to be impossible for teachers in chaotic and dangerous schools.
Can you find a scattergram of high schools (where there is more sorting)that looks that way? I can show you scattergrams of Tulsa high schools that look like scattergrams in New Jersey, where the lower right hand quarter is empty. For History, every single high school was low performing and low growth or high performing and high growth.
Bruce Baker has scattergrams that tell the same story. I think our graphics are far more common than your's. And, like I said, I'd be shocked if even Denver, which seems to be enlighten in its vam efforts, looks like the state as a whole.
And, what would your graphics look at if it wasn't math but classes that require reading comprehension? What if they showed high poverty schools taking Common Core?