The Weighting Game
A while back, I noted that states and districts should exercise caution in assigning weights (importance) to the components of their teacher evaluation systems before they know what the other components will be. For example, most states that have mandated new evaluation systems have specified that growth model estimates count for a certain proportion (usually 40-50 percent) of teachers’ final scores (at least those in tested grades/subjects), but it’s critical to note that the actual importance of these components will depend in no small part on what else is included in the total evaluation, and how it's incorporated into the system.
In slightly technical terms, this distinction is between nominal weights (the percentage assigned) and effective weights (the percentage that actually ends up being the case). Consider an extreme hypothetical example – let’s say a district implements an evaluation system in which half the final score is value-added and half is observations. But let’s also say that every teacher gets the same observation score. In this case, even though the assigned (nominal) weight for value-added is 50 percent, the actual importance (effective weight) will be 100 percent, since every teacher receives the same observation score, and so all the variation between teachers’ final scores will be determined by the value-added component.
This issue of nominal/versus effective weights is very important, and, with exceptions, it gets almost no attention. And it’s not just important in teacher evaluations. It’s also relevant to states’ school/district grading systems. So, I think it would be useful to quickly illustrate this concept in the context of Florida’s new district grading system.
In a prior post, I criticized Florida’s new formula on several grounds (I couldn’t touch on all of them in a single post). One of the issues I did not mention was this issue of nominal and effective weights.
Just to very quickly summarize, in Florida’s system, a district’s grade is calculated in an exceedingly simple manner. It is the sum of eight percentages. Four out of those eight percentages (i.e., 50 percent of a district’s final grade) are: math proficiency; reading proficiency; the percent of students “making gains” in math; and the percent of students “making gains” in reading. (As discussed in that previous post about this system, the “gains” aren’t really gains, but that’s not important for our illustrative purposes here.)
Basically, then, math and reading proficiency are worth 25 percent of a district’s final grade (12.5 percent for each subject), while the percent of students “making gains” in math and reading are also worth 25 percent (Again, 12.5 percent for each subject). The rest of the score is based on either proficiency in other subjects, or “gains” among the lowest-performing students.
But these are all the nominal weights – the ones that are assigned to each component, presumably based on their perceived importance. In this case, all four scores are deemed equally important – 12.5 percent each. But the effective weights are different. In actuality, the proficiency rates are more heavily weighted than the “gains," mostly for one simple reason: The former vary more.
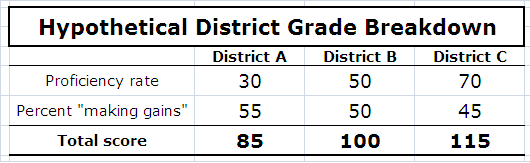
If this is confusing, here’s a simple way to look at this. Let’s say we have three districts, and their math breakdown is as follows:
The proficiency rates (first row) are 30, 50 and 70 – an average of 50, and they range between 30 and 70 (plus or minus 20 points. The "gain" scores (second row) have the same average (50), but they only vary between 45 and 55 (plus or minus 5).
When you add up the two rates for each district’s total score (bottom row), the average total is 100 (District B), plus or minus 15 points, with District A scoring 85 and District C scoring 115.
You don’t need to do any complicated calculations to understand that the proficiency rates (the first row) played the biggest part in determining differences between districts in their final scores.
For instance, District A got the highest gain score (55), but it was only five points higher than the average score of 50 (attained by District B). District C, on the other hand, got the highest proficiency rate (70), but that’s 20 points higher than the average.
Both components are, in theory (i.e., nominally), equally weighted – half and half. However, the relative “reward” for proficiency rates is greater, because there is more “space” between them. Put differently, the differences between districts’ total scores will be more heavily influenced by the proficiency rates, because the rates themselves are more different from each other.
This is basically what happens in Florida’s grading system.
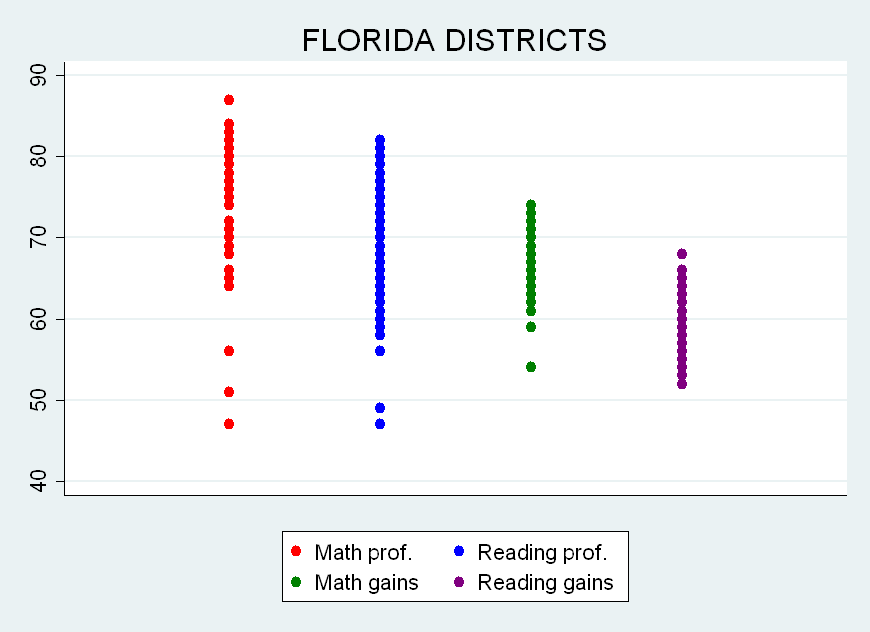
Take a look at the graph below. Each dot is one of the state’s 67 districts, and there are four groups of 67 dots, each representing components in the Florida system: math proficiency (red), reading proficiency (blue), math “gains” (green) and reading “gains” (purple).
Notice how the dots (i.e., districts) for the two “gains” measures (the two on the right, in green and purple) are more closely bunched together. That’s of course because they vary less around their average. In other words, districts vary more widely in terms of their actual rates (the two leftmost groups of dots, in red and blue) than they do in the percent of students “making gains."
Specifically, just to give you an idea, reading proficiency rates (the blue dots) vary between 47 and 82 (a 35 point spread), with an average of about 67. Reading “gains” scores (the purple dots) vary between 52 and 68 (a 16 point spread), with an average of around 60. Reading proficiency rates vary about twice as much as the "gain" scores.
Now, think about what happens when you add these two reading percentages together for each district. The variation in the total scores (proficiency plus gains) will be a function of two components: the variation in proficiency rates; and the variation in "gain" scores. If one of those components varies more than the other (as is the case), then, all else being equal, that one will make a larger contribution to the variation in final scores, even though they are theoretically (nominally) granted equal importance.
For instance, the district with the highest reading “gains” receives a score (68) that is eight points higher than the average (60), but that’s somewhat small potatoes compared with the relative “reward” that goes to the district getting the highest proficiency rate (82), which is a full 15 points higher than the average (67). These discrepancies persist throughout the distribution.
Recall the extreme hypothetical situation mentioned at the beginning of this post, in which observations and value-added count for 50 percent each, but every teacher receives the same observation score, which means that all the variation in final scores is determined by value-added. This is the same basic concept to a less extreme degree.
(Important side note: Calculating the actual effective weight for these components would also require one to account for the fact, detailed in my prior post on Florida’s system, that the proficiency rates and “gain” scores are heavily correlated with each other. In addition, variation can be both “real” and/or due to error. But, for our illustrative purposes here, we’ll just ignore these issues.)
I should point out that Florida’s system is particularly problematic in the weighting context (or particularly convenient as an illustration), since it simply adds up raw percentages as if they are directly comparable. Some other states make at least some rudimentary effort at comparability in their grading systems (e.g., converting scores to categories). But few if any do it in a manner that ensures that the effective weights are equivalent to the nominal weights, and one needs to keep this in mind when assessing the makeup of these systems.
Now, back to the original point: All of these issues also apply to teacher evaluations. You can say that value-added scores count for only 40 or 50 percent, but the effective weight might be totally different, depending both on how you incorporate those scores into the final evaluation score, as well as on how much variation there is in the other components. If, for example, a district can choose their own measures for 20 percent of a total evaluation score, and that district chooses a measure or measures that don't vary much, then the effective weight of the other components will actually be higher than it is "on paper." And the effective weight is the one that really matters.
All the public attention to weights, specifically those assigned to value-added, seem to ignore the fact that, in most systems, those weights will almost certainly be different – perhaps rather different - in practice. Moreover, the relative role – the effective weight – of value-added (and any other component) will vary not only between districts (which will have different systems), but also, quite possibly, between years (if the components vary differently each year). This has important implications for both the validity of these systems as well as the incentives they represent.
- Matt Di Carlo

Scores that vary more should be weighted higher, right?
Here's a related presentation I gave last year.
http://www.nga.org/files/live/sites/NGA/files/pdf/1107TEACHERGLAZERMAN…